Serie 01
Aus Geometrie-Wiki
Version vom 19. Oktober 2011, 19:34 Uhr von HecklF (Diskussion | Beiträge)
Inhaltsverzeichnis |
Aufgabe 1.1
- Definieren Sie für die ebene Geometrie den Begriff Bewegung
- (Definition 1.1)
Aufgabe 1.2
- Definieren Sie die Begriffe injektiv und surjektiv
Aufgabe 1.3
- Ergänzen Sie die folgende Tabelle
| Abbildung | Umkehrabbildung |
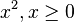 |
|
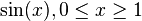 |
|
Drehung um Z mit Drehwinkel  |
|
Spiegelung an der Geraden  |
Aufgabe 1.4
- Beweisen Sie Satz 1.2
Es seien 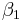 und
und 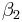 zwei Bewegungen.
zwei Bewegungen.
zu zeigen:
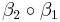 ist eine Bewegung.
ist eine Bewegung.

