12)
Aus Geometrie-Wiki
Version vom 2. Februar 2012, 16:19 Uhr von Schnirch (Diskussion | Beiträge)
Wir gehen von folgender Definition aus: Ein Drachen ist ein Viereck mit zwei Paaren jeweils zueinander kongruenter benachbarter Seiten. Beweisen Sie den folgenden Satz: Wenn 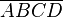 ein konvexer Drachen mit
ein konvexer Drachen mit 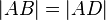 ist, dann sind die Strahlen
ist, dann sind die Strahlen 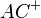 und
und 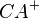 die Winkelhalbierenden von
die Winkelhalbierenden von 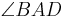 und
und 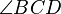 .
.

