Lösung von Aufgabe 1.3 (SoSe 12)

Welche Definition für Kreis ist richtig? Warum (nicht)?

• Sei M ein Punkt und P eine Menge, deren Elemente Punkte sind. Wenn gilt: |MP| ist konstant, so ist P ein Kreis mit Mittelpunkt M.
• Sei M ein Punkt und P eine Punktmenge. Wenn gilt: X∈P∶ |XM|= r, dann ist P ein Kreis.
• Sei M ein Punkt in der Ebene E und P eine Punktmenge. Wenn für alle X∈P gilt∶ |XM|= r, r 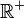$\epsilon$ $\mathbb{R}^{+}$ und X ∈ E, dann ist P ein Kreis mit dem Mittelpunkt M.
• Sei M ein Punkt in der Ebene E und P eine Menge, deren Elemente Punkte sind. Wenn für alle X∈P gilt∶ |XM|= r, r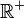$\epsilon$$\mathbb{R}^{+}$, dann ist P ein Kreis.
• Sei M ein Punkt und P eine Menge, deren Elemente Punkte sind. Alle Elemente von P liegen in ein und derselben Ebene wie M. Wenn gilt: |MP| ist konstant, so ist P ein Kreis mit Mittelpunkt M.