Lösung von Aufgabe 2.6 S (SoSe 12)

Aufgabe 2.6

Bringen Sie die folgenden Implikationen in die Form Wenn-Dann:

1. Jedes Quadrat hat vier rechte Innenwinkel.
2. Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt auf der Hypotenuse dieses Dreiecks.
3. In einem konvexen Viereck schneiden sich die Diagonalen des Vierecks.
4. Die Geraden, die durch die Diagonalen einer Raute $\overline{ABCD}$eindeutig bestimmt sind, sind Symmetrieachsen von $\overline{ABCD}$.
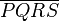5. Es sei $\overline{PQRS}$ ein Paralellogramm. Es gilt: $\angle SPQ \tilde= \angle QRS$.
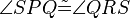6. Die Innenwinkelsumme im Dreieck beträgt 180°.

Mein Lösungsvorschlag: 1. Wenn ABCD ein Quadrat ist, dann hat es vier rechte Innenwinkel.
2. Wenn der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks bestimmt wird, dann liegt dieser auf der Hypothenuse dieses Dreiecks.
3. Wenn ein Viereck konvex ist, dann schneiden sich seine Diagonalen.
4. Wenn die Diagonalen einer Raute ABCD durch Geraden eindeutig bestimmt sind, dann sind dies Symmetrieachsen von ABCD.
5. Wenn PQRS ein Paralellogramm ist, dann sind seine Winkel SPQ und QRS konkruent zueinander.
6. Wenn ABC ein Dreieck ist, dann beträgt seine Innenwinkelsumme 180°.