Grundlagen Beweise(SoSe 12)
Wiederholung und Rückblick
Wie gehen von der folgenden Implikation aus:
Wenn das Viereck  ein Quadrat ist, dann halbieren sich seine Diagonalen.
ein Quadrat ist, dann halbieren sich seine Diagonalen.
Allgemein lässt sich eine Aussage "Wenn A dann B" schreiben als 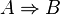 .
.
 ist dann Voraussetzung,
ist dann Voraussetzung,  ist Behauptung.
ist Behauptung.
Die Umkehrung zu einer Aussage vertauscht Voraussetzung und Behauptung.
Die Umkehrung zu 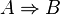 ist also
ist also 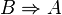 .
.
Die Umkehrung zum Beispiel lautet:
Wenn sich in einem Viereck  die Diagonalen von
die Diagonalen von  halbieren, dann ist es ein Quadrat.
halbieren, dann ist es ein Quadrat.
Aussagen können wahr oder falsch sein.
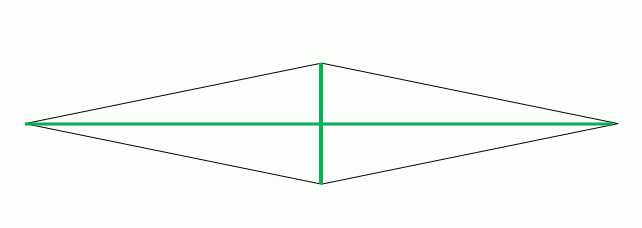
Diese Umkehrung ist falsch, was sich leicht an einem Gegenbeispiel zeigen lässt:
Nur wenn sowohl die Implikation als auch die dazugehörige Umkehrung wahr sind, lässt sich die Aussage als Äquivalenz  schreiben.
schreiben.
Sprechweise: " genau dann wenn
genau dann wenn  "
"
Im obigen Beispiel geht das NICHT!
Grundlagen des Beweisens
Wie kann eine Implikation 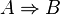 bewiesen werden?
bewiesen werden?
- direkt
- indirekt