Beweisen SoSe 12 S

Implikationen

Aus der Schule kennen Sie bereits den so genannten Wechselwinkelsatz.
Wechselwinkelsatz:
Wechselwinkel an geschnittenen Parallelen sind kongruent zueinander.

Betrachten wir diesen Satz etwas genauer: Es wird hier behauptet, dass Wechselwinkel kongruent zueinander sind (Behauptung), unter der Bedingung, dass die Wechselwinkel an geschnittenen parallelen Geraden betrachtet werden (Voraussetzung). Wir können den Satz also in eine Voraussetzung (A) und eine Behauptung (B) aufteilen.
In der Mathematik gehen wir davon aus, dass Sätze wahr sind, d. h. wenn die Voraussetzung erfüllt ist, muss auch die Behauptung notwendigerweise wahr sein.
Aussagenlogisch haben wir es somit mit einer Implikation zu tun:
formal: 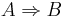$\ A \Rightarrow B$

Es seien a und b zwei verschiedene Geraden, die durch eine dritte Gerade c geschnitten werden.
Wenn zwei geschnittene Geraden paralell zueinander sind, so sind die entstehenden Wechselwinkel kongruent.--Braindead 14:33, 21. Apr. 2012 (CEST)

Wir können aus jedem Satz auch eine Umkehrung bilden (die nicht unbedingt wahr sein muss), d. h. wir formulieren die Behauptung als Voraussetzung und die Vorausetzung als Behauptung:
formal: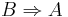$\ B \Rightarrow A$

Aufgabe: Formulieren Sie hier die Umkehrung des Wechselwinkelsatzes:

Wenn die bei dem Schnitt entstehenden Wechselwinkel kongruent sind, dann sind die Geraden a und b parallel zu einander.--Braindead 13:42, 21. Apr. 2012 (CEST)

Ist ein Satz und seine Umkehrung wahr, dann sind Voraussetzung und Behauptung äquivalent, formal kann man dann schreiben: 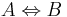$\ A \Leftrightarrow B$

Aufgabe: Formulieren Sie den Wechselwinkelsatz und seine Umkehrung in einem Satz als Äquivalenz:

Umkehrung als Äquivalenz:

Genau dann, wenn die bei dem Schnitt entstehenden Wechselwinkel kongruent zueinander sind, dann sind die Geraden a und b parallel zu einander.--Braindead 14:23, 21. Apr. 2012 (CEST)

Notwenig, hinreichend, notwendig und hinreichend

Aufgaben zum Einstieg

Zwei Paare paralleler Seiten sind notwendig, hinreichend, notwendig und hinreichend für .. ?

1. Welche der folgenden Aussagen sind wahr?
Die Eigenschaft eines Vierecks, zwei Paare paralleler Seiten zu haben, ist ...

	notwendig dafür, dass das Viereck ein Trapez ist.
	hinreichend dafür, dass das Viereck ein Trapez ist.
	notwendig und hinreichend dafür, dass das Viereck eine Trapez ist.
	ein Kriterium dafür, dass das Viereck ein Trapez ist.
	notwendig dafür, dass das Viereck ein Parallelogramm ist.
	hinreichend dafür, dass das Viereck ein Parallelogramm ist.
	ein Kriterium dafür, dass das Viereck ein Parallelogramm ist.
	notwendig und hinreichend dafür, dass das Viereck ein Parallelogramm ist.
	hinreichend dafür, dass das Viereck ein Rechteck ist.
	notwendig dafür, dass das Viereck ein Rechteck ist.
	notwendig und hinreichend dafür, dass das Viereck ein Rechteck ist.
	ein Kriterium dafür, dass das Viereck ein Rechteck ist.

Punkte: 0 / 0

Das Ganze noch mal in Wenn ... Dann ...

1. Welche Aussagen sind wahr?

	Wenn ein Viereck zwei Paare paralleler Seiten hat, dann ist es ein Trapez.
	Ein Viereck ist genau dann ein Trapez, wenn es zwei Paare paralleler Seiten hat.
	Wenn ein Viereck zwei Paare paralleler Seiten hat, dann ist es ein Parallelogramm.
	Ein Viereck ist genau dann ein Parallelogramm, wenn es zwei Paare paralleler Seiten hat.
	Wenn ein Viereck zwei Paare paralleler Seiten hat, dann ist es ein Rechteck.
	Ein Viereck ist genau dann ein Rechteck, wenn es zwei Paare paralleler Seiten hat.

Punkte: 0 / 0

Erkennen Sie den Zusammenhang?

1. Welche Aussagen sind wahr?
Die Voraussetzung in einer wahren Implikation ist immer ...

	eine notwendige Bedingung für die Behauptung der Implikation.
	eine hinreichende Bedingung für die Behauptung der Implikation.
	eine notwendige und hinreichende Bedingung für die Behauptung der Implikation.
	ein Kriterium für die Behauptung.

Punkte: 0 / 0