Funktionsrepräsentationen

In diesem Beispiel sind drei Repräsentationen der quadratischen Funktion 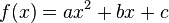$f(x)=ax^2+bx+c$ dynamisch miteinander verknüpft: Funktionsterm (links), Funktionsgraph (Mitte) und Wertetabelle (rechts). Beim Bewegen der Schieberegler verändern sich alle drei Repräsentationen simultan ("dynamic linking").

Wie baut man das?

1. Drei Schieberegler für die Parameter a-c hinzufügen (Icon "Schieberegler"; Die Position der Schieberegler kann mit dem "Bewege"-Werkzeug verändert werden, das ist der Pfeil ganz links in der Symbolleiste)
2. Unten in die Eingabezeile

   f(x)=a*x^2+b*x+c

   eingeben. Hierdurch werden die Funktion im Algebra-Teil (links) und ihr Graph (rechts) hinzugefügt.
3. Tabelle einblenden (Menü "Ansicht/Tabellenansicht")
4. In die Zelle A1 "x" eingeben (mit Anführungszeichen, damit das als Text erkannt wird) und in die Zelle B1 "f(x)"
5. In die Zellen A2, A3, ... Werte eingeben. Hierfür kann man den Zugmodus der Tabellenkalkulation nutzen: In die Zelle A2 -3 eingeben (ohne Anführungszeichen), in die Zelle A3 -2 eingeben, dann die Zellen A2 und A3 markieren, dann das kleine blaue Quadrat rechts unten in der Ecke der Markierung nach unten ziehen.
6. In die Zelle B2 folgendes eingeben: =f(A2)
7. Dann wieder den Zugmodus verwenden: Die Zelle B2 markieren, das kleine blaue Quadrat nach unten ziehen.
8. Nun ist auch die Wertetabelle fertig.
9. Mit den Schiebereglern kann man nun die Wirkung der Parameter auf den Funktionsterm, den Funktionsgraphen und die Wertetabelle untersuchen.