Basiswinkelsatz
|
Übung mit dem Classroompresenter vom 04. Mai 2012 Alle Deck'sHTML-Dokument mit allen Folien der Übung zum Durchblättern Folien aus der Übung hier einbinden:Folie im oben verlinkten html-Dokument auswählen. Rechte Maustaste drauf, Bild in neuem Tab öffnen. Dort die Adresse des Bildes auf meiner PH-Seite kopieren, Mittels iframe hier einbinden. Wie das funktioniert sehen sie im Quelltext der vorangegangenen Beispiele. ----*m.g.* 18:23, 6. Mai 2012 (CEST) (CEST) Es reicht auch aus, wenn Sie den Quelltext<iframe src="http://www.ph-heidelberg.de/wp/gieding/uebungen/04_05_12/Student Submissions_files/Student Submissions_043.png" < width="720" height="540" frameborder="2"></iframe> einfügen und nur die Nummer der Folie ändern (Student Submissions_043.png etwa in Student Submissions_045.png ändern) Viel Erfolg! Aufgabe 1AufgabenstellungMan formuliere den Basiswinkelsatz ohne die Form "Wenn-Dann" zu benutzen. Lösungsversuch 01 mit KommentarDie Folie[ www.ph-heidelberg.de is not an authorized iframe site ] KommentarDer Basiswinkelsatz wird auf der Folie zweimal formuliert. Die obere Formulierung ist korrekt. Wer ganz pingelig ist, könnte höchstens mokieren, dass es eigentlich "... zueinander kongruent." heißen müsste. Die untere Formulierung impliziert, dass alle drei Innenwinkel (s. eingekreister bestimmter Artikel) des Dreiecks zueinander kongruent sind. Das wäre dann wohl nicht korrekt.--*m.g.* 17:23, 7. Mai 2012 (CEST) Lösungsversuch 02 mit KommentarDie Folie[ www.ph-heidelberg.de is not an authorized iframe site ] KommentarAuch wenn der Begriff Basiswinkel nicht verwendet wird, geht diese Formulierung in Ordnung. Der Beweis wird zeigen, dass die beiden zueinander kongruenten Innenwinkel Basiswinkel des betrachteten Dreiecks sein müssen.--*m.g.* 17:29, 7. Mai 2012 (CEST) Lösungsversuch 03 mit KommentarDie Folie[ www.ph-heidelberg.de is not an authorized iframe site ] KommentarAuch wenn es für den Beweis eines Satzes sinnvoll sein kann, praktisch als Quintessenz die wesentlichen Aussagen zu eliminieren, die Aufgabe, den Satz zu formulieren, hat man dann natürlich nicht erfüllt.--*m.g.* 17:36, 7. Mai 2012 (CEST) Lösungsversuch 04 mit KommentarDie Folie[ www.ph-heidelberg.de is not an authorized iframe site ] KommentarHört sich ein wenig wie eine Definition an. Unterstellen wir aber, dass der Begriff gleichschenkliges Dreieck bereits definiert wurde, was natürlich vor der Formulierung des Basiswinkelsatzes geschehen sein muss, dann ist der Satz korrekt formuliert. Der unbestimmte Artikel "ein" bedeutet, dass ein beliebiges Dreieck gemeint ist. Beliebig ist so zu verstehen, dass kein gleichschenkliges Dreieck vor einem anderen gleichschenkligen Dreieck vorzuziehen ist. Letztlich sind damit alle gleichschenkligen Dreiecke gemeint. Ergo: Für alle gleichschenkligen Dreiecke gilt: es hat zwei kongruente Basiswinkel. Mitunter formuliert der Mathematiker auch mit dem bestimmten Artikel: Das gleichschenklige Dreieck hat zueinander kongruente Basiswinkel. Gemeint ist in diesem Fall die Klasse der gleichschenkligen Dreiecke. Besser: Für jeden Repräsentanten aus der Klasse der gleichschenkligen Dreiecke gilt: Die Basiswinkel sind kongruent zueinander.--*m.g.* 17:44, 7. Mai 2012 (CEST) Lösungsversuch 05 mit KommentarDie Folie[ www.ph-heidelberg.de is not an authorized iframe site ] KommentarDas ist nicht der Basiswinkelsatz, sondern seine Umkehrung.--*m.g.* 18:02, 7. Mai 2012 (CEST) Lösungsversuch 06 mit KommentarDie Folie[ www.ph-heidelberg.de is not an authorized iframe site ] KommentarDa keine Winkel eine Rolle spielen, kann es sich nicht um den Basiswinkelsatz handeln. Untersuchen wir die Formulierung trotzdem genauer. In einem Dreieck gibt es zwei kongruente Seiten versteht der Mathematiker wie folgt: Aus der Verwendung des unbestimmten Artikels folgt, dass jedes beliebige Dreieck gemeint ist. Die obige Formulierung ist damit äquivalent zu: Jedes Dreieck hat zwei kongruente Seiten. Demzufolge müsste jedes Dreieck gleichschenklig sein.--*m.g.* 18:02, 7. Mai 2012 (CEST) Lösungsversuch 07 mit KommentarDie Folie[ www.ph-heidelberg.de is not an authorized iframe site ] KommentarDie deutsche Rechtschreibung gilt auch in der Mathematik. Ansonsten ist die Formulierung absolut in Ordnung. "Im gleichschenkligen Dreieck" ist genauso wie "das gleichschenklige Dreieck" zu verstehen. Siehe hierzu den Kommentar zu Lösungvorschlag 04.--*m.g.* 18:08, 7. Mai 2012 (CEST) Lösungsversuch 08 mit KommentarDie Folie[ www.ph-heidelberg.de is not an authorized iframe site ] KommentarEs hat keinen Sinn, wenn nach dem Basiswinkelsatz gefragt ist, vorsichtshalber alles aufzuschreiben, was man zu gleichschenkligen Dreiecken weiß. Wäre unsere Aufgabe eine Klausuraufgabe und obige Lösung in der Klausur angeboten worden, gäbe es keinen einzigen Punkt dafür. Viel hilft nicht viel!--*m.g.* 18:15, 7. Mai 2012 (CEST) Aufgabe 2AufgabenstellungNennen Sie die Voraussetzung und die Behauptung sowohl vom Basiswinkelsatz als auch von dessen Umkehrung in Kurzform. Beziehen Sie sich dabei auf die Skizze. Lösungsversuch 01 mit KommentarDie Folie[ www.ph-heidelberg.de is not an authorized iframe site ] KommentarVöllig korrekt! --*m.g.* 22:28, 7. Mai 2012 (CEST) Lösungsversuch 02 mit KommentarDie Folie[ www.ph-heidelberg.de is not an authorized iframe site ] KommentarSo geht es natürlich auch. --*m.g.* 22:30, 7. Mai 2012 (CEST) Lösungsversuch 03 mit KommentarDie Folie[ www.ph-heidelberg.de is not an authorized iframe site ] KommentarSo ist es nicht ganz korrekt und das nicht wegen des fehlenden Basiswinkelsatzes. Betragsstriche bedeuten, dass es sich um eine Streckenlänge oder eine Winkelgröße handelt. Streckenlängen oder Winkelgrößen sind Zahlen. Diese werden mittels des Gleichheitszeichens in Relation gesetzt. Strecken bzw. Winkel selbst werden mittels des Zeichens für Kongruenz in Beziehung gesetzt: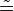 <math>\tilde=</math>.--*m.g.* 22:36, 7. Mai 2012 (CEST) Aufgabe 3AufgabenstellungFormulieren Sie die Umkehrung des Basiswinkelsatzes in "Wenn-Dann-Form". Lösungsversuch 01 mit KommentarDie Folie[ www.ph-heidelberg.de is not an authorized iframe site ] KommentarVöllig korrekt!--*m.g.* 22:49, 7. Mai 2012 (CEST) Lösungsversuch 02 mit KommentarDie Folie[ www.ph-heidelberg.de is not an authorized iframe site ] KommentarAlso, Ein gleichschenkliges Dreieck ist per Definition ein Dreieck mit zwei zueinander kongruenten Seiten. Diese Seiten werden Schenkel des gleichschenkligen Dreiecks genannt. Die Innenwinkel des Dreiecks auf deren einem Schenkel die Schenkel des gleichschenkligen Dreiecks liegen, heißen Basiswinkel des Dreiecks. Von Basiswinkeln kann man also erst dann sprechen, wenn man weiß, dass ein Dreieck gleichschenklig ist. Setzt man zunächst wie bei der Umkehrung des Basiswinkelsatzes nur voraus, dass ein Dreieck zwei kongruente Innenwinkel hat, ist streng genommen zunächst nicht klar, dass das Dreieck gleichschenklig ist. Gleichschenklige Dreiecke und nur gleichschenklige Dreiecke haben Basiswinkel. Spreche ich in der Voraussetzung der Umkehrung des Basiswinkelsatzes von Basiswinkeln, impliziert dieses Formulierung unmittelbar, dass es sich um ein gleichschenkliges Dreieck handelt. Also: Wenn ein Dreieck gleichschenklig ist, dann ist es gleichschenklig. Typischer Fall von: Wenn du kein iPhone hast, dann hast du kein iPhone. --*m.g.* 22:49, 7. Mai 2012 (CEST) |

