Definieren der Relation "Parallel" auf der Menge aller Geraden

Übung mit dem Classroompresenter vom 11. Mai 2012 Alle Deck's HTML-Dokument mit allen Folien der Übung zum Durchblättern Folien aus der Übung hier einbinden: Folie im oben verlinkten html-Dokument auswählen. Rechte Maustaste drauf, Bild in neuem Tab öffnen. Dort die Adresse des Bildes auf meiner PH-Seite kopieren, Mittels iframe hier einbinden. Wie das funktioniert sehen sie im Quelltext der vorangegangenen Beispiele. --*m.g.* 19:34, 21. Apr. 2012 (CEST) Es reicht auch aus, wenn Sie den Quelltext <iframe src="http://www.ph-heidelberg.de/wp/gieding/uebungen/11_05_12/Student Submissions_files/Student Submissions_043.png" width="720" height="540" frameborder="2"></iframe> einfügen und nur die Nummer der Folie ändern (Student Submissions_043.png etwa in Student Submissions_045.png ändern) Viel Erfolg! Aufgabe 1 Aufgabenstellung Formulieren Sie Überschriften für die Spalten der Tabelle. Kommentierte Lösungsversuche Lösung 1 [ www.ph-heidelberg.de is not an authorized iframe site ] Die Identität von Geraden ist ein Spezialfall der Parallelität. Macht es Sinn, die Identität explizit in die Spaltenüberschrift zu integrieren?--*m.g.* 09:41, 15. Mai 2012 (CEST) Lösung 2 [ www.ph-heidelberg.de is not an authorized iframe site ] So geht das in Ordnung. Vielleicht wäre es noch bessser anstelle von "geschnittene Geraden" "sich schneidende Geraden zu formulieren.--*m.g.* 09:50, 15. Mai 2012 (CEST) Lösung 3 [ www.ph-heidelberg.de is not an authorized iframe site ] Korrekt! Natürlich hätte ich lieber die Spaltenüberschrift "sich schneidende Geraden" gehabt. Bei offenen Aufgabenstellungen muss man mit solchen Ergebnissen leben.--*m.g.* 09:50, 15. Mai 2012 (CEST) Aufgabe 2 Aufgabenstellung Definieren Sie die Relation Parallel auf der Menge der Geraden der Ebene. Kommentierte Lösungsversuche Lösung 1 [ www.ph-heidelberg.de is not an authorized iframe site ] Das ist nur die halbe Wahrheit. Auch wenn die Geraden identisch sind, gelten sie als parallel. Man mag sich fragen, welchen Sinn es hat, die Identität als Parallelität zu akzeptieren. Das Ganze erschließt sich erst, wenn man sich genauer mit Relationen beschäftigt. Von besonderer Bedeutung sind die sogenannten Äquivalenzrelationen. Zu den notwendigen eigenschaften von Äquivalenzrelationen gehört die Reflexivität. Im speziellen Fall bedeutet das, dass jede Gerade zu sich selbst parallel ist.--*m.g.* 13:56, 15. Mai 2012 (CEST) Lösung 2 [ www.ph-heidelberg.de is not an authorized iframe site ] Erkennen Sie, warum die Identität in dieser Formulierung aufgehoben ist?--*m.g.* 14:00, 15. Mai 2012 (CEST) Lösung 3 [ www.ph-heidelberg.de is not an authorized iframe site ] Ebenso korrekt. Lediglich das Wort "zusammen" würde ich durch "gemeinsam" ersetzen. Zusammen deutet mehr auf die Idee der Vereinigungsmenge hin. Wir brauchen aber die Schnittmenge. Lösung 4 [ www.ph-heidelberg.de is not an authorized iframe site ] Identität?--*m.g.* 14:07, 15. Mai 2012 (CEST) Aufgabe 3 Aufgabenstellung= Definieren Sie die Relation "parallel" auf der Menge aller Geraden der Ebene unter Verwendung des Begriffs Schnittmenge. 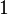Lösung 1 [ www.ph-heidelberg.de is not an authorized iframe site ] $g$ ist eine Menge von Punkten, $h$ ist eine Menge von Punkten, ist die Menge die aus der natürlichen Zahl $1$ besteht. Wie soll durch das Schneiden zweier Mengen, die nur aus Punkten bestehen, eine Menge entstehen, die aus einer Zahl besteht? Gemeint war sicherlich Folgendes: $\left|g \cap h \right| \not= 1$ Lösung 2 [ www.ph-heidelberg.de is not an authorized iframe site ] Genau dasselbe wie bei Lösung 1 nur in Textform. Lösung 3 [ www.ph-heidelberg.de is not an authorized iframe site ] Nicht einen Punkt gemeinsam haben bedeutet, dass die Geraden entweder keinen oder unendlich viele Punkte gemeinsam haben. Also das logische und muss durch ein logisches oder ersetzt werden und dann ist da noch das problem mit den unendlich vielen gemeinsamen Punkten. ist da absolut nicht korrekt.