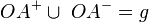Zusatzaufgaben 7 S (SoSe 12)
Aus Geometrie-Wiki
Version vom 31. Mai 2012, 16:07 Uhr von Buchner (Diskussion | Beiträge)
Zusatzaufgabe 7.1
Gegeben sei ein Dreieck  und eine Gerade g.
und eine Gerade g.
Behauptung: Wenn g eine Seite von  schneidet, dann schneidet g genau eine weitere Seite von
schneidet, dann schneidet g genau eine weitere Seite von  .
.
a) Vergleichen Sie diese Behauptung mit dem Axiom von Pasch. Wo liegt der Unterschied?
b) Widerlegen Sie die Behauptung durch eine Skizze.
Lösung von Zusatzaufgabe 7.1_S (SoSe_12)
Zusatzaufgabe 7.2
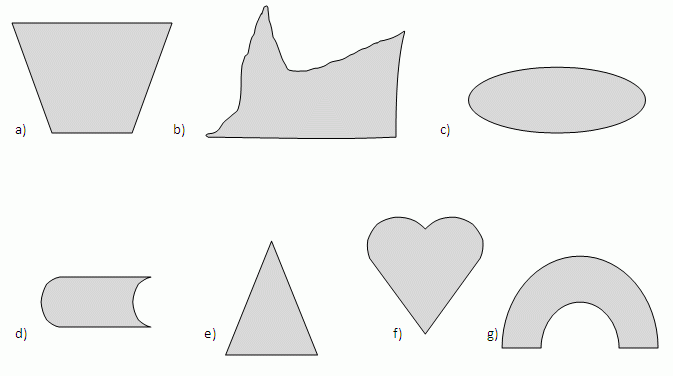
Die grauen Flächen seien Punktmengen (Teilmengen einer Ebene). Welche Figuren sind konvex? Warum (nicht)?
Lösung von Zusatzaufgabe 7.2_S (SoSe_12)
Zusatzaufgabe 7.3
Beweisen Sie: Ist O ein beliebiger Punkt einer Geraden g und A ein weiterer (von O verschiedener) Punkt dieser Geraden, so gilt für die Halbgeraden 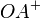 und
und 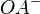 :
:
a) 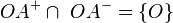
b)