Lösung von Aufgabe 6.1P (SoSe 12)

Beweisen Sie: Aus $\operatorname{Zw} \left( A, B, C \right)$ folgt $\operatorname{koll} \left( A, B, C \right)$.

Nr.	Beweisschritt	Begründung
1)	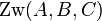$\operatorname{Zw} (A,B,C)$	Vor.
2)	$\left| AB \right| +\left| BC \right| = \left|AC \right|$	def. zwischenrelation
3)	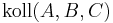$\operatorname{koll}(A,B,C)$	dreiecksungleichung (axiom II/3)

--Studentin 13:47, 3. Jun. 2012 (CEST) So kann man es machen.--Tutorin Anne 15:33, 6. Jun. 2012 (CEST)

Ich kann nicht verstehen, ob die Kollineation mit Vektoren zusammenhängt und ob bei der Kollineationsdefinition alle drei Gleichungen erfüllt sein müssen oder nur noch eins davon: /AB/ + /BC/= /AC/, /AC/ +/CB/ = /AB/, /BA/ + /AC/ = /BC/.

nur eine der drei Gleichungen--Tutorin Anne 15:33, 6. Jun. 2012 (CEST)

Anders gesagt was ist damit gemeint: /AB/ + /BC/= /AC/ die Länge der Strecke AC?

ich weiß nicht, ob dies deine frage beantwortet:--Studentin 15:44, 5. Jun. 2012 (CEST)
Alles klar oder gibt's noch Fragen?--Tutorin Anne 15:33, 6. Jun. 2012 (CEST)