Lösungsidee Übung Heckl 06.06.2012 5.2 S

Aufgabe 5.2

Diese Aufgabe war letzte Woche noch zu schwer- sorry dafür. Versuchen Sie es diese Woche nochmal.
Zeigen Sie, dass für drei paarweise verschiedene Punkte $\ A, B$ und $\ C$ gilt:
$\operatorname Zw (A, B, C)$ $\Rightarrow$ $\overline{AB}$ $\subset$ $\overline{AC}$

Zunächst eine Skizze

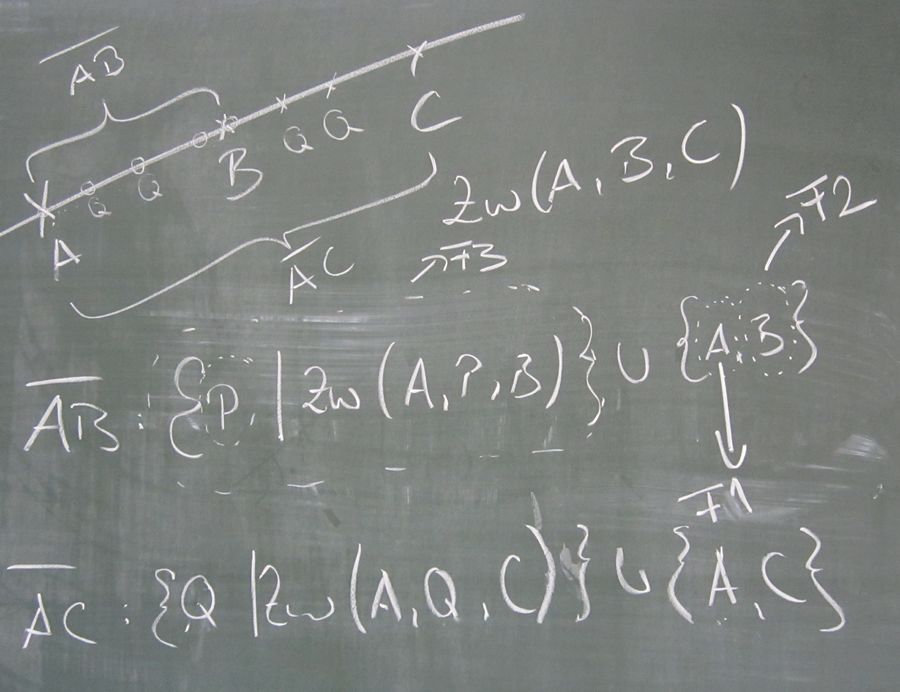
Nachdem wir uns die Voraussetzung und die Behauptung angeschrieben hatten, machten wir uns anhand dieser Skizze (Definition der beiden Strecken) klar, warum wir drei Fälle unterscheiden müssen. F1,F2 und F3 stehen dabei für die drei Fälle 1-3.

Der Beweis

Schritt 1

Voraussetzung, Behauptung und Fall 1 mit 2.

Schritt 2

Fall 3 ist etwas aufwendiger: Wir führen auf zwei potentielle Zwischenrelationsmöglichkeiten zurück! Wenn wir in Schritt (1) bereits von einem Strahl $\ AB^{+}$ ausgehen, fällt es uns noch einfacher - das geht wegen 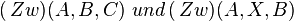$\operatorname(Zw) (A, B, C) \ und \operatorname(Zw) (A, X, B)$ in der Voraussetzung.

Schritt 3

Wir zeigen in einem Widerspruchsbeweis, dass 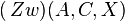$\operatorname(Zw) (A, C, X)$ nicht sein kann und führen dies zum Widerspruch.

Schritt 4

Wir lagern Teilbeweis II nochmals aus - aus Gründen der Übersichtlichkeit. Dadurch, dass wir gezeigt haben, dass 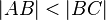$|AB| < |BC|$ gilt, haben wir automatisch auch gezeigt, dass 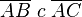$\overline{AB} \ c \ \overline{AC}$ ECHTE Teilmenge ist.



--Flo60 20:16, 6. Jun. 2012 (CEST)

Zurück zur Übungsseite

Übung_Aufgaben_6_S (SoSe_12)