Lösung von Zusatzaufgabe 8.4 S
Inhaltsverzeichnis |
Die Aufgabe
Seien 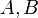 und
und  drei paarweise verschiedene Punkte für die gelte
drei paarweise verschiedene Punkte für die gelte 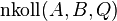 . Sei g eine Gerade. Beweisen Sie:
. Sei g eine Gerade. Beweisen Sie:
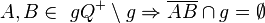 .
.
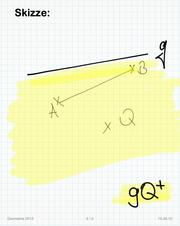
Skizze
Voraussetzung, Behauptung
Voraussetzung:
- (V1)
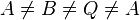
- (V2)
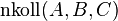
- (V3) Gerade g
- (V4)
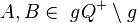
- (V1)
Behauptung:
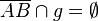
Beweis folgt..
--Tchu Tcha Tcha 19:22, 15. Jun. 2012 (CEST)
Bemerkungen M.G.
Damit sind die Grundlagen für den Beweis korrekt gelegt.
Beweis durch Widerspruch
Annahme
Beweis:
| Nr. | Beweischritt | Begründung | Bemerkung M.G. |
|---|---|---|---|
| 1) | 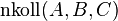 |
Voraussetzung | korrekt, vielleicht genauer (V2) |
| 2) | Es existiert ein Dreieck 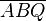 |
(1) | besser: Es existiert das Dreieck 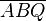 . Die drei Punkte . Die drei Punkte 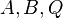 waren jetzt ja bestimmt. Weil sie nicht kollinear sind, sind sie die Eckpunkte eines Dreiecks. Siehe Definition des Begriffs Dreieck, muss hier aber nicht mehr explizit aufgeführt werden. waren jetzt ja bestimmt. Weil sie nicht kollinear sind, sind sie die Eckpunkte eines Dreiecks. Siehe Definition des Begriffs Dreieck, muss hier aber nicht mehr explizit aufgeführt werden.
|
| 3) | 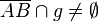 |
(Annahme) | korrekt |
| 4) | 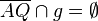 und und 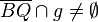 oder 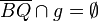 und und 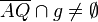 |
Axiom von Pasch | Das ist so korrekt. Besser wäre es noch, wenn Schritt 3) mit zur Begründung angegeben wird. Letztlich können wir ja nur deshalb behaupten, dass eine weitere Seite von 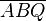 durch durch  geschnitten wird, weil bereits eine Seite nach Schritt 3) durch geschnitten wird, weil bereits eine Seite nach Schritt 3) durch  geschnitten wird. geschnitten wird. Für unseren Beweis wäre es aber auch ausreichend zu schreiben, dass jetzt 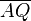 oder oder 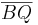 durch durch  geschnitten werden. geschnitten werden.Also: 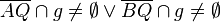 Es ist natürlich richtig, dass wenn etwa 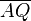 durch durch  geschnitten wird geschnitten wird 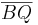 nicht mehr durch nicht mehr durch  geschnitten werden kann, für unseren Beweis ist das jedoch belanglos. geschnitten werden kann, für unseren Beweis ist das jedoch belanglos.
|
| 5) | Widerspruch zur Voraussetzung: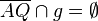 und und 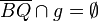 (4), Vor: (4), Vor: 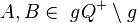 |
.. | Das ist so korrekt. Weil unsere beiden Punkte Punkte  und und  ja mit dem Punkt ja mit dem Punkt  bezüglich bezüglich  in derselben Halbebene liegen, kann weder die Strecke in derselben Halbebene liegen, kann weder die Strecke 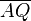 noch die Strecke noch die Strecke 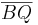 entsprechend der Definition offene Halbebene mit entsprechend der Definition offene Halbebene mit  einen Punkt gemeinsam haben. einen Punkt gemeinsam haben.
|
5) Widerspruch zur Voraussetzung: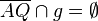 und
und 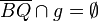 (4), Vor:
(4), Vor: 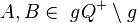
Behauptung folgt ! 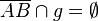
--a.b.701 13:40, 16. Jun. 2012 (CEST)
________________________________________________________________________________________________________________________________________________________ @a.b.701: A)Muss in der Begründung in deinem Schritt 1 neben der Vor. nicht auch noch Def. I/2 stehen? B)Folgt dann im Schritt 2 logisch, dass die Punkte A,B,C ein Dreieck bilden? Oder muss man hier noch einen Zwischenschritt machen. Vielleicht über die Dreiecksungleichung als Begründung? --Luca123 18:37, 17. Jun. 2012
Ich hätte in Schritt 1 auch zusätzlich noch die Def. I/2 dazu geschrieben. Ich denke aber, dass es nicht zwingend notwendig ist, da es sich hier in diesem Fall nur aus der Voraussetzung ergibt. (?)--Sissy66 23:51, 17. Jun. 2012 (CEST)