Lösung von Aufgabe 6.4
Beweisen Sie: Jede Ebene enthält wenigstens drei paarweise verschiedene Punkte.
Behauptung: Wenn eine Ebene E existiert, dann enthält sie wenigstens drei paarweise verschiedene Punkte A, B, C. Vorraussetzung: Es existiert eine Ebene E mit A, B, C Element E Annahme: A, B, C sind paarweise verschieden.
| Beweisschritt | Begründung |
| (1) komp (A,B,C) (2) A nicht identisch B B nicht identisch C C nicht identlich A || 1)nach Definition I/6 |
=> A, B, C sind paarweise verschieden
Kommt uns ein wenig zu kurz vor. von Maude001 und Nicola
Inhaltsverzeichnis |
Behauptung:
Wenn eine Ebene E existiert, dann enthält sie wenigstens drei paarweise verschiedene Punkte A, B, C.
Vorraussetzung:
Es existiert eine Ebene E mit A, B, C 
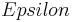
Annahme:
A, B, C sind paarweise verschieden.
Diesen Satz I.7 ("Jede Ebene enthält (wenigstens) drei Punkte.") muss man bestimmt mit einer Fallunterscheidung beginnen.
Fall 1:
koll(A, B, C) <-> A, B, C  Gerade g
Dadurch ergibt sich ja (nach Vorraussetzung), dass A, B, C
Gerade g
Dadurch ergibt sich ja (nach Vorraussetzung), dass A, B, C 
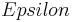 und (nach Fallunterscheidung) A, B, C
und (nach Fallunterscheidung) A, B, C  g. Dann greift Axiom I/5
g. Dann greift Axiom I/5
Wenn zwei Punkte einer Geraden g in einer Ebene E liegen, so gehört g zu E.
...hier sind es sogar alle drei Punkte.
Fall 2:
Je zwei Punkte sind nichtkollinear.
o.B.d.A koll(A, B) -> nkoll(A, C)  nkoll(B, C)
nkoll(B, C)
AXIOM I/1(Axiom von der Geraden)
Zu zwei beliebigen verschiedenen Punkten gibt es genau eine Gerade, die die beiden Punkte enthält.
(Deswegen brauchen wir auch den Fall 3 nicht, wonach alle drei Punkte nichtkollinear sind. Geht nicht!)

