Lösung von Aufgabe 10.4P (SoSe 12)
Aus Geometrie-Wiki
Version vom 2. Juli 2012, 15:45 Uhr von Knechtk (Diskussion | Beiträge)
Beweisen Sie Satz IX.3:
Bei einer Punktspiegelung ist der Schnittpunkt S der beiden Spiegelgeraden a und b Mittelpunkt der Strecke 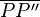 , mit
, mit 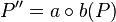 .
.
Vor.: a verkettet b (P)=P ´´, a geschnitten b = S
Beh: S ist Mittelpunkt von PP``, also: PS=P´´S
1. In der Vorlesung haben wir bereits bewiesen: Jeder Punkt liegt mit seinem Bildpunkt P´´= a verkettet b (P) auf einem Kreis um S. Also SP=SP´´ (Def. Mittelpunkt)
2. P und P´´ sind e K, PSP´´ ist Durchmesser
nur weil P und P´´ auf dem Kreis liegen ist die Verbindung ja noch kein Durchmesser. Der Beweis ist nur richtig, wenn du diesen Schritt auch begründen kannst.--Tutorin Anne 15:26, 2. Jul. 2012 (CEST)
Das kann man doch mit Hilfe der Eigenschaft "streckentreue der Geradespiegelung" erkläre oder? so wäre das die Strecke P'S gleich der strecke PS und damit liegt S in der Mitte der Strecke P'P?[[]]
3. S ist Mittelpunkt von PP´´ (2.1.) q.e.d.--Geogeogeo 13:17, 2. Jul. 2012 (CEST)

