Der Zusammenhang von Seitenlängen und Winkelgrößen im Dreieck (SoSe 12)
Inhaltsverzeichnis |
Satz IX.2: (Der größeren Seite liegt der größere Winkel gegenüber)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen.
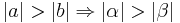
- Es sei
Beweis von Satz IX.2
Es sei  ein Dreieck.
ein Dreieck.
Voraussetzung:
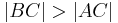 bzw.
bzw. 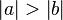
Behauptung:
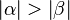
Die folgenden Hilfskonstruktionen liefern die Beweisidee (kommentieren Sie die Abbildungen und führen Sie den Beweis):
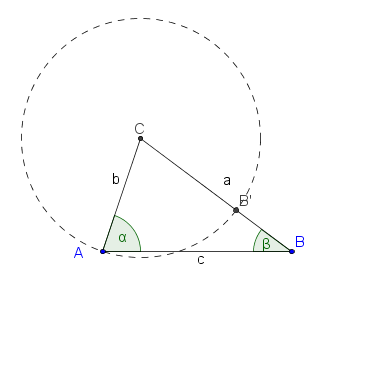
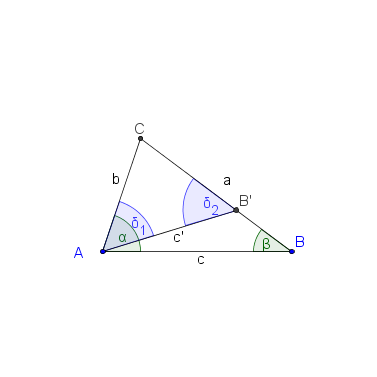
Frage zur Beweisführung:
In der heutigen Geometrie Veranstaltung haben wir den Schritt (3) 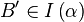 anhand der Konvexität begründet..
anhand der Konvexität begründet..
Mich würde interessieren, ob ich es auch anhand vom Lemma 1 begründen kann, da ich mir damit einfacher tue..!??
Lemma 1 besagt doch folgendes:
Gegeben seien drei nicht kollineare Punkte (hier A, B, C / nach Voraussetzung). Wenn B' (nach Konstruktion..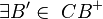 ) ein Punkt der offenen Strecke (hier:
) ein Punkt der offenen Strecke (hier: 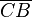 / nach Konstruktion) ist, dann liegt der Strahl (hier
/ nach Konstruktion) ist, dann liegt der Strahl (hier 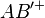 ) vollständig im Inneren von
) vollständig im Inneren von 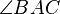 .
.
Also müsste doch bei Schritt (3), Lemma 1 als Begründung korrekt sein..!?
--Tchu Tcha Tcha 12:21, 5. Jul. 2012 (CEST)
Satz IX.3: (Dem größeren Winkel liegt die größere Seite gegenüber)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen. 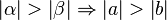
- Es sei
Beweis von Satz IX.3
Übungsaufgabe

