Lösung von Aufg. 11.7 S
Aufgabe 11.7
Definieren Sie: Stufenwinkel, Wechselwinkel, entgegengesetzt liegende Winkel.
Definitionsversuch Nummero6/Tchu Tcha Tcha:
Def. (Stufenwinkel):
Es seien g und h zwei zueinander parallele Geraden, die von einer dritten Gerade i geschnitten werden.
Wenn gilt:
- Fehler beim Parsen(Syntaxfehler): \ g \cap i = \{S_1} \wedge \ h \cap i = \{S_2}
und
-
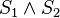= Scheitelpunkte von 2 Winkeln und
- (3) jeweils genau ein Schenkel dieser beiden Winkel liegt in ein und derselben Halbebene bezüglich der Geraden i und
- (4) jeweils der andere Schenkel dieser beiden Winkel ist Teilmenge der Geraden i, wobei einer dieser beiden Schenkel auch Teilmenge des anderen Schenkels sein muss
,dann nennt man diese Winkel, Stufenwinkel.
Def. (Wechselwinkel):
(Voraussetzung: Stufenwinkel wurde bereits definiert und darf in der Definition verwendet werden..)
Es seien 
und 
Stufenwinkel.
Wenn 
der Scheitelwinkel von ist,
dann ist der Wechselwinkel von .
Def. (entgegengesetzte Winkel):
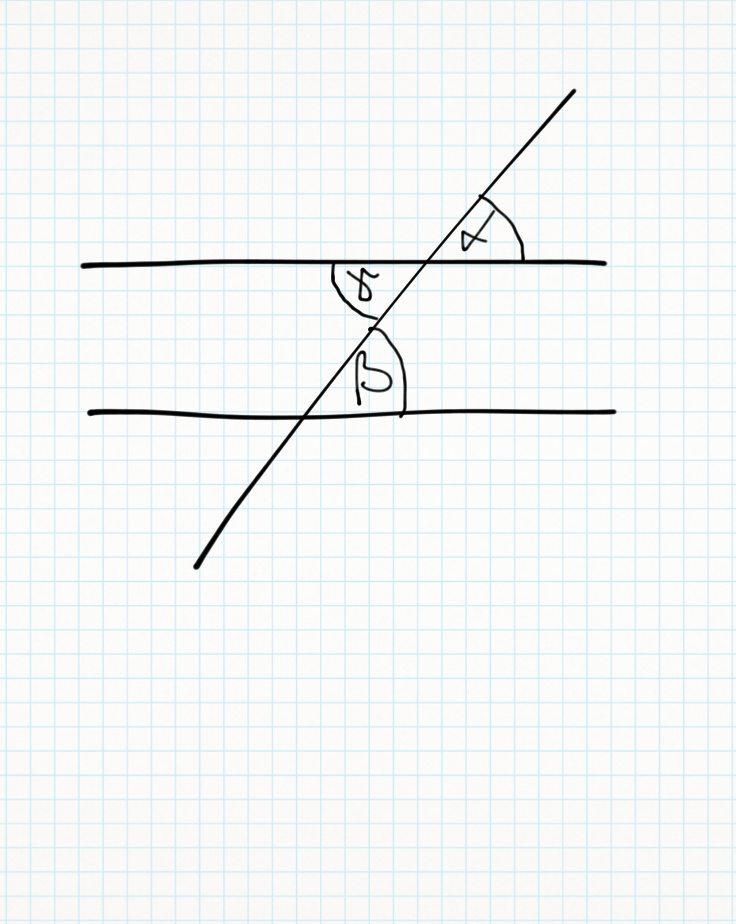
Es seien g und h zwei zueinander parallele Geraden, die von einer dritten Gerade i geschnitten werden.
Wenn gilt:
- Fehler beim Parsen(Syntaxfehler): \ g \cap i = \{S_1} \wedge \ h \cap i = \{S_2}
und
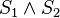- = Scheitelpunkte von 2 Winkeln und
- beide Winkel liegen in der selben Halbebene bezüglich i und
- beide Winkel liegen auf verschiedenen Seiten der Halbebene bezüglich g und/oder h
,dann nennt man diese Winkel, entgegengesetzte Winkel.
--Tchu Tcha Tcha 11:16, 8. Jul. 2012 (CEST)
Zur Definition:Stufenwinkel --> Deine Definition wäre ja nur ein Spezialfall, dass die Winkel auch noch gleich groß sind (siehe Stufenwinkelsatz) Es gibt aber auch Stufenwinkel an nicht parallelen Geraden. --Funkdocta 13:18, 8. Jul. 2012 (CEST)
Stimmt. Hast Du einen Vorschlag?--Tchu Tcha Tcha 13:30, 9. Jul. 2012 (CEST)
Wäre der Wechselwinkel von Alpha auch der Scheitelwinkel von Beta?--RitterSport 17:21, 11. Jul. 2012 (CEST)
