Satz: Asteroiden besitzen (wenigstens) die gleichen Spiegelachsen wie ein Quadrat

Satz

Sei a eine Asteroide. Die Schnittpunkte der Asteroide a mit dem Umkreis seien folgend mit A, B, C, D bezeichnet.
Für alle Spiegelachsen, die das Viereck $\overline{ABCD}$ auf sich selbst abbildet gilt: Alle diese Achsen bilden auch die Asteroide a auf sich selbst ab.

Beweis

Teil 1: Zeige, dass $\overline{ABCD}$ ein Quadrat ist

Nach Konstruktion unserer Asteroide liegen alle Punkte des Vierecks auf einem Kreis. Man kann entweder mit dem Satz des Pythagoras die Seitenlängen ausrechnen und ins Verhältnis zueinanderstellen.
Aus Gründen der Einfachheit wird hier einfach mit der Definition Quadrat argumentiert - gleich lange, sich schneidende Diagonalen, die senkrecht stehen und sich gegenseitig halbieren.

Teil 2

Zeige, dass DB spiegelachse der Asteroide ist

Bei 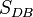$S_{DB}$ sind per Definition D und B Fixpunkte. Nach Konstruktion unserer Asteroide (und auch aus dem Quadrat) gilt, dass auch A auf C und umgekehrt abgebildet wird.
Nun gilt noch für die restlichen Punkte der Asteroide zu zeigen, dass die Punkte auf sich selbst abgebildet werden:
Ich versuche den Beweis mal so zu führen, wie er glaube ich sinnvoll ist - vllt. kann Hr. Gieding dazu einen Kommentar hinterlassen, ob das so sauber ist!

Wir wählen uns irgendeinen beliebigen Punkt P auf der Asteroide (ich orientiere mich an der Skizze - es gilt dies o. B. d. A. und P ist f. a. b.). Nach unserer Konstruktion der Asteroide existiert nun ein (eindeutiger) Winkel 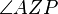$\angle AZP$, der aus der Drehung unserer Asteroide enstand.
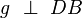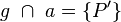Ferner gilt nun, dass eine Gerade g existiert, für die gilt, dass $g \ \perp \ DB$ und $\ g \ \cap \ a = \left\{ P' \right\}$ Aus Gründen der Übersichtlichkeit nennen wir den Schnittpunkt von g und DB S.
Wenn es mir nun gelingt zu zeigen, dass 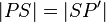$|PS| = |SP'|$ gilt, bin ich fertig.

Ich weiß, dass auch der Winkel 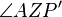$\angle AZP'$ existiert und 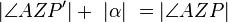$|\angle AZP'| + \ |\alpha| \ = |\angle AZP|$ ist (nach Konstruktion Asteroide.
(ZWISCHENSPEICHERN)