Satz: Asteroiden besitzen (wenigstens) die gleichen Spiegelachsen wie ein Quadrat

Satz

Sei a eine Asteroide. Die Schnittpunkte der Asteroide a mit dem Umkreis seien folgend mit A, B, C, D bezeichnet.
Für alle Spiegelachsen, die das Viereck $\overline{ABCD}$ auf sich selbst abbildet gilt: Alle diese Achsen bilden auch die Asteroide a auf sich selbst ab.

Beweis

Teil 1: Zeige, dass $\overline{ABCD}$ ein Quadrat ist

Nach Konstruktion unserer Asteroide liegen alle Punkte des Vierecks auf einem Kreis. Man kann entweder mit dem Satz des Pythagoras die Seitenlängen ausrechnen und ins Verhältnis zueinanderstellen.
Aus Gründen der Einfachheit wird hier einfach mit der Definition Quadrat argumentiert - gleich lange, sich schneidende Diagonalen, die senkrecht stehen und sich gegenseitig halbieren.

Teil 2

Zeige, dass DB spiegelachse der Asteroide ist

Bei 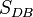$S_{DB}$ sind per Definition D und B Fixpunkte. Nach Konstruktion unserer Asteroide (und auch aus dem Quadrat) gilt, dass auch A auf C und umgekehrt abgebildet wird.
Nun gilt noch für die restlichen Punkte der Asteroide zu zeigen, dass die Punkte auf sich selbst abgebildet werden:
Ich versuche den Beweis mal so zu führen, wie er glaube ich sinnvoll ist - vllt. kann Hr. Gieding dazu einen Kommentar hinterlassen, ob das so sauber ist!

Wir wählen uns irgendeinen beliebigen Punkt P auf der Asteroide (ich orientiere mich an der Skizze - es gilt dies o. B. d. A. und P ist f. a. b.). Nach unserer Konstruktion der Asteroide existiert nun ein (eindeutiger) Winkel 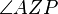$\angle AZP$, der aus der Drehung unserer Asteroide enstand.
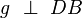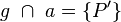Ferner gilt nun, dass eine Gerade g existiert, für die gilt, dass $g \ \perp \ DB$ und $\ g \ \cap \ a = \left\{ P' \right\}$ Aus Gründen der Übersichtlichkeit nennen wir den Schnittpunkt von g und DB S.
Wenn es mir nun gelingt zu zeigen, dass 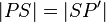$|PS| = |SP'|$ gilt, bin ich fertig.

Nehmen wir dazu an, dass die Streckenlängen nicht gleich lang sind.
Dann existiert auf unserer Asteroide ein Punkt P* mit der Eigenschaft, dass 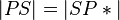$|PS| = |SP*|$ ist. Jetzt ist das Dreieck 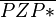$\overline{PZP*}$ ein gleichschenkliges (wegen Kongruenzssatz SWS sind die beiden Teildreiecke kongruent) Dreieck.
Ferner gilt, dass die Winkel 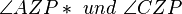$\angle AZP* \ und \ \angle CZP$ gleich groß sind (Rechnen in |R, NW 180, Kongruenz der Dreiecke). Zudem gilt auch, dass die Länge der Strecken 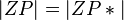$|ZP| = |ZP*|$ gilt.
Nach unserer Konstruktion der Asteroide a muss nun aber gelten, dass P* = P' ist. Dieser Beweisteil wird erneut mittels Dreieckskongruenzen geführt und ausgelagert:

Zunächst noch die bisherige Skizze:

Ausgelagerter Beweisteil

Wir betrachten dazu mal folgendes: Sehen wir zunächst einfach mal davon ab, dass sich innerhalb des großen Kreises ein weiterer kleinerer dreht, dann gilt doch, dass unser sich drehender Ausgangspunkt (sei dies A) auf dem großen Kreis verbleibt. Die Winkel 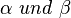$\alpha \ und \ \beta$ sind (wie vorher gezeigt) kongruent zueinander.
Damit jetzt A auf A' abgebildet wird, wird nach der Konstruktion der Asteroide der Punkt A um den Winkel Alpha gedreht. Damit Punkt A auf den Punkt C abgebildet wird, muss der Punkt A noch um Beta gedreht werden (bei gleichem Drehzentrum, logischerweise).

OK, habe grad festgestellt, dass auch dieser Ansatz zu verwerfen ist, weil A' und P* nur dann auf dem gleichen Strahl liegen, wenn Alpha gleich 45 (oder 90) - was irgendwie auch logisch ist, bei Betrachtung der kleinen Kreisdrehung.

Jetzt mag ich nicht mehr :-) --Flo60 20:02, 12. Jul. 2012 (CEST)
Jetzt mag ich wieder - ich habe mir die Lösung eigentlich gerade selbst konstruiert und sie liegt direkt vor meinen Augen (und zwar der GANZE Beweis):

Nochmal von vorne

Weil 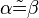$\alpha \tilde {=} \beta$ (nach Konstruktion, Erläuterung siehe oben) und 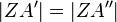$|ZA'| = |ZA''|$, sowie 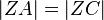$|ZA| = |ZC|$ (Konstruktion am Kreis) gilt nach SWS, dass auch $|AA'| = |CA''|$.

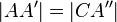Wir wissen ferner, dass 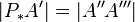$|P_*A'| = |A''A'''|$ gilt (nach Konstruktion Asteroide - Durchmesser kleiner Kreis.

Weil nun P* so entsteht, dass es eine Drehung um einen k mit dem Drehwinkel 4*Alpha entsteht Punkt A auf einer ähnlichen Bahn ensteht (gleicher Kreis, gleicher Drehwinkel - Länge ist also identisch, auch die Krümmung). Aus diesem Grunde folgt, dass auch 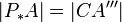$|P_*A| = |CA'''|$ gilt.
Nun sind auch die kleinen grünen Dreiecke kongruent zueinander. Bei Spiegelung an DB kann nun nur noch P* auf A abgebildet werden. --Flo60 20:26, 12. Jul. 2012 (CEST)

Zurück zur Übersichtsseite

Übungsveranstaltung Elementargeometrie 2012