Lösung von Aufg. 12.3 S
Beweisen Sie: Wenn  ein Punkt außerhalb der Geraden
ein Punkt außerhalb der Geraden  ist, dann gibt es eine Gerade
ist, dann gibt es eine Gerade  , die durch
, die durch  geht und parellel zu
geht und parellel zu  ist.
ist.
Lösungsversuch Nummero6/Tchu Tcha Tcha:
Vor.: Gerade g, Punkt 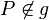
Beh.: Es gibt eine Gerade  , die durch
, die durch  geht und parellel zu
geht und parellel zu  ist.
ist.
Annahme: Es gibt KEINE Gerade  , die durch
, die durch  geht und parellel zu
geht und parellel zu  ist.
ist.
(1) 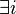 : Fehler beim Parsen(Syntaxfehler): P \in i \wedge i \not \equiv g \wedge \ i \cap g = \{S}
: Fehler beim Parsen(Syntaxfehler): P \in i \wedge i \not \equiv g \wedge \ i \cap g = \{S}
mit dem Schnittpunkt
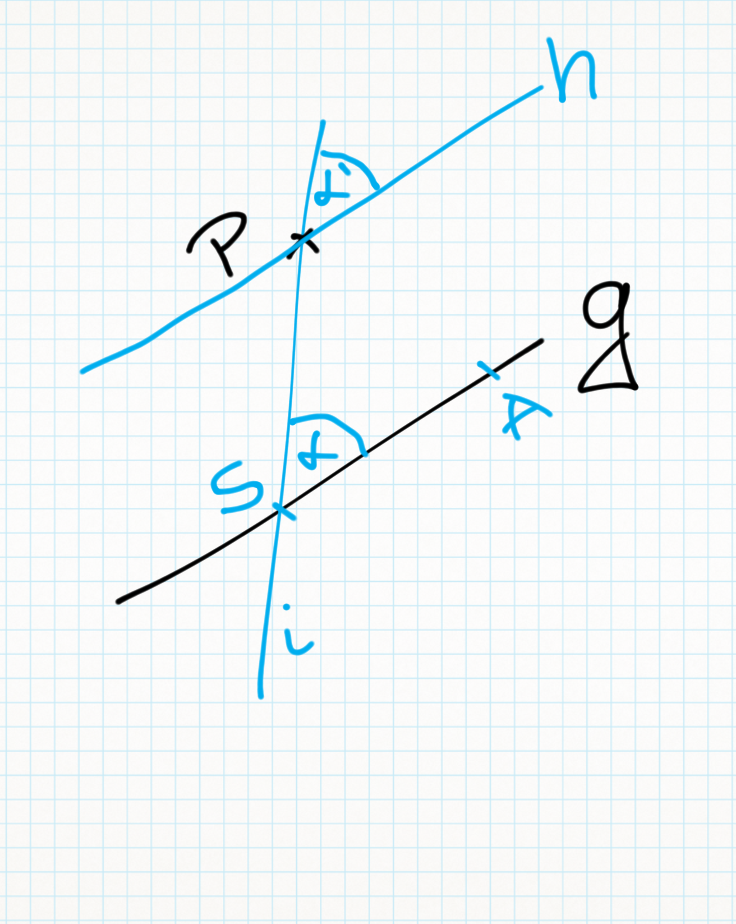
(2) 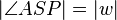 // (1),Winkelmaßaxiom (ab sofort gilt zur Vereinfachung, vgl. Skizze,
// (1),Winkelmaßaxiom (ab sofort gilt zur Vereinfachung, vgl. Skizze,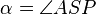 )
)
(3) Es gibt einen Winkel 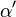 in der Halbebene
in der Halbebene 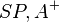 für den gilt:
für den gilt: 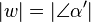 // Winkelkonstruktionsaxiom (2), Voraussetzung
// Winkelkonstruktionsaxiom (2), Voraussetzung
(4) 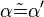 // (1-3), Def. Stufenwinkel
// (1-3), Def. Stufenwinkel
(5) 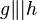 // (4), Umkehrung des Stufenwinkelsatzes
// (4), Umkehrung des Stufenwinkelsatzes
(6) Widerspruch zur Annahme // (5)
(7) Behauptung stimmt // (6)
qed
--Tchu Tcha Tcha 16:28, 13. Jul. 2012 (CEST)


