Lösung von Testaufgabe 2.3 SS12
Vor.: P \neq A, P\neq B, P\in AB+ Beh.: P\not\in AB- Ann.: P\in AB-
(1) Es gilt Zw (A,P,B) oder Zw (A,B,P) Vor., Def. Strahl (2) Zw (P,A,B) Annahme (3) IPAI+IABI=IPBI (2), Def. Zwischenrelation (4) IAPI+IPBI=IABI o.B.d.A. (1), Def. ZWischenrelation (5) IPAI+IAP+IPBI=IPBI (3),(4), Rechnen in R (6) 2IPAI = 0 (5), Rechnen in R (7) P=A Widerspruc zur Vor., dass gilt P\neq A Axiom II/1, (Axiom II/2 ?) Annahme ist zu verwerfen, Beh. stimmt --*osterhase* 17:33, 14. Jul. 2012 (CEST)
Gehört der Punkt P zur Halbgeraden AB+, gilt nach der Definition Halbgerade AB+, entweder Zw(A,P,B) oder Zw(A,B,P).
Würde Zw(P,A,B) gelten, ist P nach Definition AB- nicht mehr auf der Halbgeraden AB+ sondern auf der Halbgeraden AB-.
Somit kann der Punkt P nicht auf beiden Halbgeraden liegen.
Laut Voraussetzung gehört der Punkt P zur Halbgeraden  .
.
Da wir ebenfalls wissen, dass 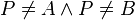 muss für P nach der Definition
muss für P nach der Definition  gelten:
gelten:
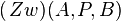 oder
oder 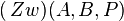 und somit kann der Punkt P, nach der Definition von
und somit kann der Punkt P, nach der Definition von 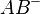 ,
nicht auch zu
,
nicht auch zu 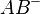 gehören.--Tchu Tcha Tcha 18:39, 14. Jul. 2012 (CEST)
gehören.--Tchu Tcha Tcha 18:39, 14. Jul. 2012 (CEST)

