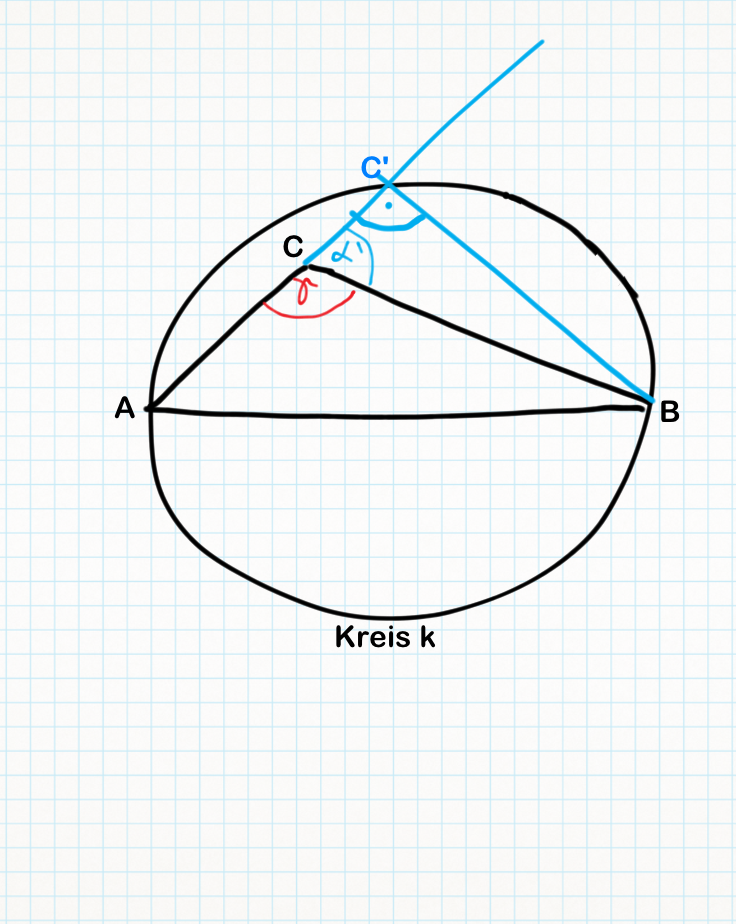
Lösung von Testaufgabe 2.4 SS12
Lösungsversuch Nummero6/Tchu Tcha Tcha:
Voraussetzung: Kreis k mit Durchmesser 
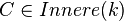
Behauptung: 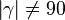
Annahme: 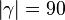
(1) 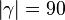 // Annahme
// Annahme
(2) 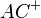 muss den Kreis k in einem weiteren Punkt C' (oBdA) schneiden, da nach Voraussetzung C im Inneren von k liegt und
muss den Kreis k in einem weiteren Punkt C' (oBdA) schneiden, da nach Voraussetzung C im Inneren von k liegt und 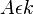 (Durchmesser)
(Durchmesser)
(3) 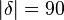 // Vor., (2), Satz des Thales
// Vor., (2), Satz des Thales
(4) 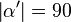 // (1), Def. NW, Def. suppl., Supplementaxiom, Def. rechter Winkel
// (1), Def. NW, Def. suppl., Supplementaxiom, Def. rechter Winkel
(5) Widerspruch (zum Korollar 1) im Dreieck 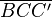 // (2),(3),Korollar 1 (mindestens 2 Innenwinkel sind spitz)
// (2),(3),Korollar 1 (mindestens 2 Innenwinkel sind spitz)
(6) 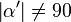 // (5)
// (5)
(7) 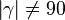 // (6), Def.NW, Def. suppl.,Supplementaxiom, Rechnen in R
// (6), Def.NW, Def. suppl.,Supplementaxiom, Rechnen in R
(8) Widerspruch zur Annahme // (7)
(9) Behauptung stimmt // (8)
q.e.d.
--Tchu Tcha Tcha 19:06, 14. Jul. 2012 (CEST)
Vor. Kreis k mit Durchmesser AB, Punkt C im Inneren von k
Beh. 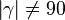
Annahme: 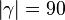
1. Punkt C im Inneren von k / Vor.
2. Es existiert ein Schnittpunkt C' von AC+ auf k / 1.
3. < AC'B wäre somit = 90 / 2. , Satz des Thales
4. < ACB = 90 / Annahme
5. < ACB somit Außenwinekl von Dreieck ACB und < AC'B ein nichtanliegender Innenwinkel von Dreieck ACB / 2. Def. Innenwinkel, Def. Außenwinkel
6. Wiederspurch zum schwachen Außenwinkelsatz, da Innenwinkel < AC'B genauso groß wie der Außenwinkel <ACB wäre. / 3., 4., 5.
7. Die Annahme ist zu verwerfen und die Behauptung stimmt.