Lösung von Aufgabe 3.6 P (SoSe 12)
Aus Geometrie-Wiki
Version vom 15. Juli 2012, 11:22 Uhr von Hakunamatata (Diskussion | Beiträge)
Satz: Gegeben sei ein Dreieck  in einer Ebene E und eine Gerade g in dieser Ebene, die keine der drei Punkte A, B und C enthält.
Wenn g die Strecke
in einer Ebene E und eine Gerade g in dieser Ebene, die keine der drei Punkte A, B und C enthält.
Wenn g die Strecke  schneidet, so schneidet sie auch entweder die Strecke
schneidet, so schneidet sie auch entweder die Strecke  oder die Strecke
oder die Strecke  .
.
a) Wie lautet die Kontraposition dieser Implikation?
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?
_________________________
a) Kontraposition: Gerade g schneidet nicht  und g schneidet nicht
und g schneidet nicht 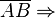 g schneidet nicht
g schneidet nicht 
- Diese Kontraposition ist nicht vollständig. Warum?--Tutorin Anne 11:43, 8. Mai 2012 (CEST)
Weil noch ausgeschlossen werden muss, das die Gerade nicht durch die Eckpunkte verläuft?! [--Hakunamatata 12:22, 15. Jul. 2012 (CEST)]
b) Annahme: Gerade g schneidet nicht  und g schneidet nicht
und g schneidet nicht 
von --Honeydukes 23:29, 4. Mai 2012 (CEST)
- Gilt hier auch - so stimmt's noch nicht ganz.--Tutorin Anne 11:43, 8. Mai 2012 (CEST)

