Lösung von Zusatzaufgabe 12.1P (SoSe 12)
Beweisen Sie Satz XIV.2 (Dem größeren Winkel liegt die größere Seite gegenüber). Hinweis: Sie dürfen Satz XIV.1 als bekannt voraussetzen.
Der Beweis sieht vielleicht schwierig aus und klingt auch so, weil er als Zusatzaufgabe ausgeschrieben ist, ist er aber nicht. Wichtig ist es den Hinweis zu beachten und dann ist auch gar nicht mehr so viel zu tun! Also nur Mut!--Tutorin Anne 09:27, 10. Jul. 2012 (CEST)
Vor: | |>|
|>| |
|
Beh: |a|>|b|
Ann. |a|<|b|
1.) | |<|
|<| | |Ann. Satz XIV.1
| |Ann. Satz XIV.1
 Widerspruch zur Voraussetzung...
Widerspruch zur Voraussetzung...
So einfach kann es niemals sein :D
(Toni wenn das stimmt kannst du den Beweis niemals führen ;-) )
- Der Beweis ist schon ganz gut, nur.... nicht komplett und damit noch nichts bewiesen, denn die Annahme ist nicht richtig (komplett).--Tutorin Anne 12:55, 16. Jul. 2012 (CEST)
Mathematik ist nicht nur schön, sondern manchmal auch einfach. Auf den obigen Beweis trifft beides zu, finden Sie nicht?--Schnirch 12:00, 16. Jul. 2012 (CEST)
Das ist mir vorher auch aufgefallen :-(
Die Annahme müsste |a|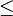 |b| heißen
|b| heißen
Dann wäre das, was ich oben gemacht habe Fall 1.
Fall 2 wäre |a|=|b|, daraus folgt | |=|
|=| |, was dann ein Widerspruch zur Voraussetzung sein müsste, oder?
|, was dann ein Widerspruch zur Voraussetzung sein müsste, oder?
--Jussuf Ölkan 19:29, 16. Jul. 2012 (CEST)
Richtig! Lediglich noch die Begründung fehlt, weshalb | |=|
|=| | folgt.--Tutorin Anne 14:40, 18. Jul. 2012 (CEST)
| folgt.--Tutorin Anne 14:40, 18. Jul. 2012 (CEST)
Hier mal ein direkter Versuch:
Beh. |a|>|b| bzw. |BC|>|AC|
1.) Konstruktion eines Kreises mit dem Radius CA um den Punkt C (Konstruktion)
2.) CA geschnitten k = {B'} (1, Konstruktion)
3.) |CA|=|CB'| (Def. Kreis, 2.)
4.) CB'+B'B = CB (Zwischenrelation(C,B',B))
5.) CA+B'B = CB (3. in 4. einsetzten)
6.) |CA|<|BC| und somit auch a>b (5.)
Kommt das so auch hin, obwohl ich die Voraussetzung gar nicht richtig verwende?! Ist vom Prinzip her wie der Beweis des Satzes XIV.1 aufgebaut.. -- Menolly 18:06 19. Jul. 2012 (CEST)

