Lösung von Aufgabe 9.3P (SoSe 12)

Beweisen Sie die Winkeltreue der Geradenspiegelung. Nutzen Sie für den Beweis die Halbgeradentreue und die Eigenschaft der Geradenspiegelung winkelmaßerhaltend zu sein.

Vielleicht ist es eine doofe Frage, aber was ist der Unterschied zwischen winkelmaßerhaltend und Winkeltreue?--Zitrone 12:35, 24. Jun. 2012 (CEST)

Hei, ich glaube dass die Eigenschaft der Winkeltreue über die "Winkelerhaltung" zu beweisen ist. Ich meine, dass Herr Schnirch am vergangenen Dienstag gesagt hat, dass "winkelerhaltend" ein Axiom ist. Wir können also die Winkeltreue beweisen, indem wir uns auf das Axiom der "Winkelerhaltung bei Geradenspiegelungen" beziehen. --Honeydukes 12:14, 25. Jun. 2012 (CEST)

• winkelerhaltend - festgelegte Eigenschaft der Geradenspiegelung (- ein Axiom) Danke Honeydukes! Dabei handelt es sich um das Maß der Winkel, dass gleich bleibt.
• winkeltreu meint dabei, dass auch die Schenkel des Winkels wieder Schenkel sind, also die Abbildung des Winkels auch wirklich wieder ein Winkel und nicht z.B. zwei lose Strecken ergibt.--Tutorin Anne 11:44, 26. Jun. 2012 (CEST)

mir geht es ähnlich wie zitrone. ich weiß auch nicht den unterschied.
ich wäre daher über einen anderen ansatz gegangen:
wenn ich drei nicht lineare punkte a, b, s habe, kann ich ja die beiden halbgeraden sa+ und sb+ betrachten mit winkel asb.
beide halbgeraden werden halbgeradentreu abgebildet, wie wir in aufgabe 9.1 festgestellt haben.
außerdem wissen wir, dass die drei strecken sa, sb und ab streckentreu abgebildet werden.
können wir dann nicht sagen, dass wenn die beiden dreiecke sab und s'a'b' kongruent sind, die winkeltreue gilt?
wahrscheinlich nicht, oder?
--Studentin 01:52, 26. Jun. 2012 (CEST)
Ja, so lässt es sich nicht begründen. Aber der Ansatz über die Halbgeraden ist gut.--Tutorin Anne 11:44, 26. Jun. 2012 (CEST)

Ich hab keine Ahnung ob das, was ich gerechnet habe, stimmt. Hier mein Vorschlag ;)

(1) AS+ -> A'S'+ und BS+ -> B'S'+ ; Def. Halbgeradentreue

(2) AS+ geschnitten mit BS+ = {S} mit <ASB ; (1), Def. Winkel

(3) Sg (<ASB) => <A'S'B' ; (2), Axiom bzw. Eigenschaft Winkelmaßerhaltend

Erklärung(sversuch): Da ein Winkel aus zwei Halbgeraden besteht, werden alle Punkte gemäß der Halbgeradentreue auch auf der Spiegelung der Halbgeraden, eingeschlossen dem gemeinsamen Schnitt- bzw Anfangspunkt S, abgebildet. Nach Def. Winkel ergeben die beiden Halbgeraden den Winkel und somit gilt auch hierfür die Spiegeltreue aller Punkte, also bleibt die Winkelgröße gleich. --fahrtwind


Mein neuer Versuch:

Vor: $\angle ABC, Sg(A)=A', Sg(B)=B', Sg(C)=C'$
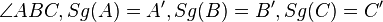
Beh: $Sg(\angle ABC ) = \angle A'B'C'$

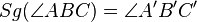
Beweisschritt	Begründung
1 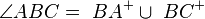$\angle ABC = \ BA^{+} \cup \ BC^{+}$	(Vor, Def. Winkel)
2 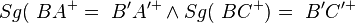$Sg(\ BA^{+} = \ B'A'^{+} \wedge Sg (\ BC^{+}) = \ B'C'^{+}$ )	(Halbgeradentreue, 1, Vor.)
3 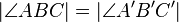$|\angle ABC| = |\angle A'B'C'|$	(Winkelmaßerhaltend (Eig. Geradenspiegelung))
4 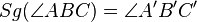$Sg(\angle ABC ) = \angle A'B'C'$	(1,2,3)

--Fahrtwind 23:08, 19. Jul. 2012 (CEST)