Lösung von Aufgabe 7.1
Aus Geometrie-Wiki
Version vom 11. Juni 2010, 18:21 Uhr von Maude001 (Diskussion | Beiträge)
Beweisen Sie: Zu jeder Strecke  existiert genau eine Strecke
existiert genau eine Strecke  mit
mit  und
und  .
.
mal ein Anfang:
Behauptung: es existiert genau eine Strecke  mit
mit  und
und 
Es müssen zwei Beweise geführt werden:
1. Existenz
2. Eindeutigkeit
Beweis 1:
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | es ex. d 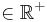 : d= : d= 
|
Axiom II.1 |
| (II) | es ex. d*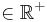 : d*= : d*= 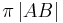 = =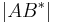
|
Axiom II.1, Rechnen in 
|
| (III) | d < d* | 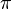 und d sind positiv und d sind positiv
|
| (VI) |
Irgendwie verstricke ich mich. Wer mag weitermachen, oder neu anfangen? --Maude001 17:21, 11. Jun. 2010 (UTC)

