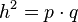Lösung Aufgabe 2.5 WS 12 13
Aus Geometrie-Wiki
Version vom 6. November 2012, 22:19 Uhr von B..... (Diskussion | Beiträge)
Aufgabe 2.5Der Satz des Pythagoras sei bewiesen. Es sei
Wir gehen davon aus, dass Beweisen Sie den Höhensatz von Euklid:
Lösung von User: ...
Lösung von User: ...--B..... 22:19, 6. Nov. 2012 (CET)
|
 ein Dreieck mit den schulüblichen Bezeichnungen:
ein Dreieck mit den schulüblichen Bezeichnungen: liegt die Seite
liegt die Seite  gegenüber, dem Punkt
gegenüber, dem Punkt  die Seite
die Seite und dem Punkt
und dem Punkt  die Seite c.
die Seite c.
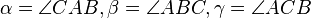 .
.
 der rechte Winkel ist.
der rechte Winkel ist. 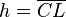 sei das Lot von
sei das Lot von  . Der Fußpunkt
. Der Fußpunkt  des Lotes von
des Lotes von 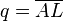 und
und 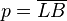 .
.