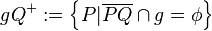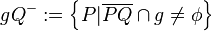Halbebenen und der Satz von Pasch WS 12 13
Inhaltsverzeichnis |
Halbebenen und der Satz von Pasch
Halbebenen
Analogiebetrachtungen
| |
|
Definition des Begriffs der Halbebene
Alles hat zwei Seiten oder grundlegende Ideen der Beschaffenheit von Ebenen
Offene Halbebenen
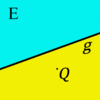
Die beiden Seiten, in die die Menge der Punkte einer Ebene  , die nicht auf einer Geraden
, die nicht auf einer Geraden  dieser Ebene liegen, durch diese Gerade
dieser Ebene liegen, durch diese Gerade  eingeteilt wird, heißen offene Halbebenen von
eingeteilt wird, heißen offene Halbebenen von  bezüglich der Trägergeraden
bezüglich der Trägergeraden  . Der nicht zu
. Der nicht zu  gehörende Referenzpunkt
gehörende Referenzpunkt 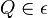 bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich
bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich  mit
mit  auf derselben Seite liegen, wird mit
auf derselben Seite liegen, wird mit  bezeichnet, die andere offene Halbebene von
bezeichnet, die andere offene Halbebene von  bezüglich
bezüglich  und
und  mit
mit  .
.
Obige Ausführungen können als informelle Definition des Begriffs offene Halbebene dienen. Hinsichtlich wirklicher mathematischer Exaktheit der Festlegung, was denn eine offene Halbene sein möge, bedarf es einer genauereren Erklärung, was denn darunter zu verstehen wäre, dass zwei Punkte  und
und  einer Ebene
einer Ebene  auf ein und derselben bzw. auf zwei verschiedenen Seiten dieser Ebene bezüglich einer Geraden
auf ein und derselben bzw. auf zwei verschiedenen Seiten dieser Ebene bezüglich einer Geraden  liegen.
liegen.
Definition II.1: (offene Halbebene)
- Es sei
 eine Ebene in der die Gerade
eine Ebene in der die Gerade  liegen möge. Ferner sei
liegen möge. Ferner sei  ein Punkt der Ebene
ein Punkt der Ebene  , der nicht zur Geraden
, der nicht zur Geraden  gehört.
gehört.
Unter den offenen Halbebenen und
und  bezüglich der Trägergeraden
bezüglich der Trägergeraden  versteht man die folgenden Teilmengen der Ebene
versteht man die folgenden Teilmengen der Ebene  ohne die Gerade
ohne die Gerade  :
:
- Es sei
Halbebenen
Vereinigt man die Menge der Punkte einer offenen Halbeben mit der Menge der Punkte der Trägergerade so erhält man eine Halbebene.
Definition II.2: (Halbebene)
- Es sei
 eine Gerade der Ebene
eine Gerade der Ebene  .
.  und
und 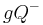 seien die beiden offenen Halbebenen von
seien die beiden offenen Halbebenen von  bezüglich
bezüglich  . Unter den (geschlossenen) Halbebenen von
. Unter den (geschlossenen) Halbebenen von  bezüglich
bezüglich  versteht die beiden Punktmengen, die durch die Vereinigung jeder dieser beiden offenen Halbebene von
versteht die beiden Punktmengen, die durch die Vereinigung jeder dieser beiden offenen Halbebene von  bezüglich der Geraden
bezüglich der Geraden  mit jeweils dieser Geraden
mit jeweils dieser Geraden  entstehen.
entstehen.
- Es sei
Bemerkung: Für die formale Beschreibung von offenen und geschlossenen Halbebenen wird jeweils dieselbe Bezsichnung verwendet: offene Halbebene:  , (geschlossene) Halbebene:
, (geschlossene) Halbebene:  . Der weitere Gebrauch der Sprache kennzeichnet, ob es sich um eine offene oder um die geschlossene Halbene handeln soll. Aus Gründen der Vereinfachung sei vereinbart, dass
. Der weitere Gebrauch der Sprache kennzeichnet, ob es sich um eine offene oder um die geschlossene Halbene handeln soll. Aus Gründen der Vereinfachung sei vereinbart, dass  bzw.
bzw. 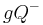 immer die geschlossene Halbebene meint. Soll die offene Halbebene gemeint sein, so ist dieses durch den Zusatz "offen" zu kennzeichnen.
immer die geschlossene Halbebene meint. Soll die offene Halbebene gemeint sein, so ist dieses durch den Zusatz "offen" zu kennzeichnen.
Definition II.3: Halbraum
Gegeben sei eine Ebene E und ein Raum R, der E enthält. Die Punkte des Raumes, die nicht in E liegen, bilden zwei Mengen derart, dass gilt:
- Offener Halbraum
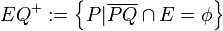
- Offener Halbraum
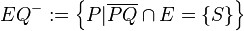
- Offener Halbraum
Der Satz von Pasch
Satz II.1: Der Satz von Pasch
- Gegeben sei ein Dreieck
 . Ferner sei
. Ferner sei  eine Gerade, die durch keinen der drei Eckpunkte
eine Gerade, die durch keinen der drei Eckpunkte  geht. Wenn
geht. Wenn  eine der drei Seiten des Dreiecks
eine der drei Seiten des Dreiecks  schneidet, dann schneidet
schneidet, dann schneidet  genau eine weitere Seite des Dreiecks
genau eine weitere Seite des Dreiecks  .
.
- Gegeben sei ein Dreieck
Beweis des Satz von Pasch
Übungsaufgabe
Konvexe Punktmengen
Definition II.4: (konvexe Punktmenge)
- Eine Menge
 von Punkten heißt konvex, wenn mit je zwei Punkten
von Punkten heißt konvex, wenn mit je zwei Punkten  und
und  dieser Menge die gesamte Strecke
dieser Menge die gesamte Strecke  zu
zu  gehört.
gehört.
- Eine Menge
Satz II.2
- Halbebenen sind konvexe Punktmengen
Beweis von Satz II.2
trivial (Der Leser überzeuge sich davon)
Satz II.3
- Der Durchschnitt zweier konvexer Punktmengen ist konvex.
Beweis von Satz II.3
Es seien  und
und 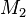 zwei konvexe Mengen.
zwei konvexe Mengen.
zu zeigen: Der Durchschnitt der beiden Mengen  und
und 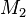 ist auch konvex.
ist auch konvex.
 gehört u.a., dass jede Gerade
gehört u.a., dass jede Gerade 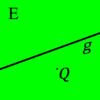
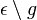 , die mit
, die mit