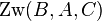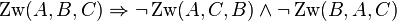|
Aufgabe 6.1
Satz:
- Es seien
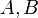 und und  drei paarweise verschiedene Punkte. drei paarweise verschiedene Punkte.
- Wenn der Punkt
 zwischen den Punkten zwischen den Punkten  und und  liegt, dann liegt weder liegt, dann liegt weder  zwischen zwischen  und und  noch noch  zwischen zwischen  und und  . .
Beweisen Sie diesen Satz.
Lösung 6.1 von User Hazel12

Bemerkungen Sissy66
Ich denke, dass die Voraussetzung ist, dass die 3 Punkte paarweise verschieden sind, also:
Vor: A,B,C sind paarweise verschieden
Beh: Zw(A,B,C)
Ann: Zw(A,B,C) und (oBdA.) Zw(B,A,C)
Wenn man doch oBdA. hinschreibt, muss man den zweiten Teil des Beweises nicht mehr machen, oder?--Sissy66 14:23, 2. Dez. 2012 (CET)
m.g.
@Sissy66
- Eine Implikation kann mehrere Voraussetzungen haben. Im speziellen Fall wäre eine Voraussetzung, dass die drei Punkte paarweise verschieden sind , was noch...?--*m.g.* 13:29, 3. Dez. 2012 (CET)
- o.B.d.A. passt nicht ganz, wenn die Aufgabe so formuliert ist, wie sie hier formuliert wurde. Siehe Bemerkungen zu Hazel.
- Formulieren Sie die Aufgabe so, dass o.B.d.A. korrekt wäre.--*m.g.* 16:26, 3. Dez. 2012 (CET)
@Hazel12
Die Implikation
Wir setzen voraus, dass für die Punkte 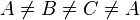 gilt. gilt.
- Formulierung der Implikation in der Aufgabe:
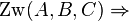 weder weder 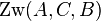 noch noch 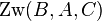
- Ihre Formulierung der Implikation:
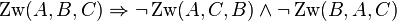
- Fazit: Sie haben das weder noch gut umgesetzt
Die Beweisführung
korrekt
Es wäre ausreichend, den Beweis nur für einen Fall zu formulieren. Fall 2: analog.
Warum wäre o.B.D.A, in unserem Fall nicht korrekt?
Frage: Können wir davon ausgehen, dass die 3 Punkte (A;B;C) kollinear sind?
Und stimmt die Begründung "Def. Zwischenrelation"? Müsste die Begründung nicht "Umkehrung der Zwischenrelation" heißen?
--Caro44 17:42, 5. Dez. 2012 (CET)
|
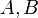 und
und  drei paarweise verschiedene Punkte.
drei paarweise verschiedene Punkte. zwischen den Punkten
zwischen den Punkten  und
und 
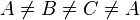 gilt.
gilt.
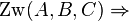 weder
weder 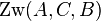 noch
noch