Lösung von Aufgabe 7.7 WS 12 13
Aus Geometrie-Wiki
Version vom 10. Dezember 2012, 18:10 Uhr von Tutorin Anne (Diskussion | Beiträge)
Aufgabe 7.7Es sei BemerkungUnter fast allen versteht der Mathematiker alle bis auf endlich viele.
Lösung von User ...Mal einen Versuch. Könnte die Zeichnung so stimmen? Bin mir unsicher. --Yellow 12:06, 10. Dez. 2012 (CET) Lösung von User ... |
 eine Strecke.
eine Strecke. 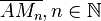 ist eine Folge von Strecken mit
ist eine Folge von Strecken mit 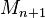 ist der Mittelpunkt von
ist der Mittelpunkt von 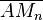 . Beweisen Sie: Für jedes
. Beweisen Sie: Für jedes 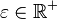 gilt: Fast alle Folgeglieder von
gilt: Fast alle Folgeglieder von  mit
mit 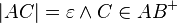 .
.


