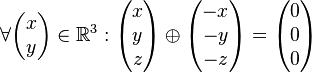Die abelsche Gruppe der geordneten Tripel reeller Zahlen 2012 13
Aus Geometrie-Wiki
Version vom 12. Dezember 2012, 19:21 Uhr von *m.g.* (Diskussion | Beiträge)
Die nichtleere Menge
Die additive VerknüpfungFehler beim Parsen(Lexikalischer Fehler): \forall \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix}, \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} \in \mathbb{R}^3: \begin{pmatrix} x_1 \\ y_1 \\z_1 \end{pmatrix} \oplus \begin{pmatrix} x_2 \\ y_2 \\ z_2\end{pmatrix}= \begin{pmatrix} x_1+x_2 \\ y_1+y_2 \\ z_1 + z_2\end{pmatrix}\
Abgeschlossenheit der additiven Verknüpfung
|
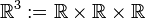
 auf
auf 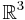

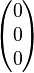 leistet das Verlangte. (Überzeugen Sie sich davon.)
leistet das Verlangte. (Überzeugen Sie sich davon.)