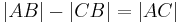Lösung von Aufgabe 6.9
Inhaltsverzeichnis |
Vorlage
Satz:
- Von drei paarweise verschiedenen Punkten
 und
und  ein und derselben Geraden
ein und derselben Geraden  liegt genau einer zwischen den beiden anderen.
liegt genau einer zwischen den beiden anderen.
- Von drei paarweise verschiedenen Punkten
Beweisen Sie diesen Satz.
Lösung --Schnirch 13:50, 16. Jun. 2010 (UTC)
Satz in wenn-dann:
- Wenn drei Punkte
 und
und  kollinear sind, dann liegt genau einer zwischen den beiden anderen Punkten.
kollinear sind, dann liegt genau einer zwischen den beiden anderen Punkten.
- Wenn drei Punkte
Beweis
Es seien also  und
und  drei Punkte.
drei Punkte.
Voraussetzungen:
koll( und
und  )
)
Behauptung
- es gilt genau eine der drei möglichen Zwischenrelationen:
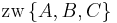 oder
oder 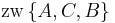 oder
oder 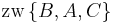
- es gilt genau eine der drei möglichen Zwischenrelationen:
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 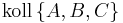
|
Voraussetzung |
| (II) | es gilt eine der drei Gleichungen:
|
(I), Axiom II/3 |
| (III) | 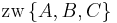 oder oder 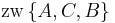 oder oder 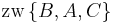
|
(II), Def (Zwischenrelation) |
| (IV) | zu zeigen: es liegt genau einer zwischen den beiden anderen
| |
| (V) | 
|
(IV), (Axiom II/3) |
| (VI) | 
|
rechnen mit reellen Zahlen, (Axiom II/2) |
| (VII) | 
|
(VI gleichgesetzt), rechnen mit reellen Zahlen |
| (VIII) | 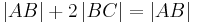
|
(VII), + 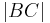
|
| (IX) | 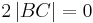
|
(VIII), - 
|
| (X) | Widerspruch, da die beiden Punkte B und C identisch sein müssten, nach Voraussetzung aber drei verschiedene Punkte A, B und C gegeben sind.
|
vorausgegangene Diskussion
Versuch I
Satz:
- Von drei paarweise verschiedenen Punkten
 und
und  ein und derselben Geraden
ein und derselben Geraden  liegt genau einer zwischen den beiden anderen.
liegt genau einer zwischen den beiden anderen.
- Von drei paarweise verschiedenen Punkten
Beweisen Sie diesen Satz.
Satz in wenn-dann:
- Wenn drei Punkte
 und
und  kollinear sind, dann liegt genau einer zwischen den beiden anderen Punkten (und umgekehrt???) .
kollinear sind, dann liegt genau einer zwischen den beiden anderen Punkten (und umgekehrt???) .
- Wenn drei Punkte
Beweis
Es seien also  und
und  drei Punkte.
drei Punkte.
Voraussetzungen:
koll( und
und  )
)
Behauptung
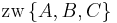 oder
oder 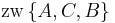 oder
oder 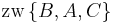
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 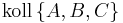
|
Voraussetzung |
| (II) | Für drei beliebige Punkte  und und  gilt: gilt: 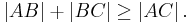
|
Axiom II/3: (Dreiecksungleichung) |
| (III) | 
|
Axiom II/3.1
|
| (IV) | ||
| (V) |
...und jetzt? --Heinzvaneugen
Ich glaube, es ist noch zu zeigen, dass genau einer zwischen den beiden anderen liegt. Habe deinen Beweis ab Schritt IV weitergeführt:
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (IV) | 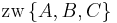 oder oder 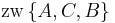 oder oder 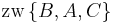
|
Def (Zwischenrelation) |
| (V) | zu zeigen: es liegt genau einer zwischen den beiden anderen
| |
| (VI) | 
|
(Axiom II/3) |
| (VII) | 
|
rechnen mit reellen Zahlen, (Axiom II/2) |
| (VIII) | 
|
(VII gleichgesetzt), rechnen mit reellen Zahlen |
| (IX) | 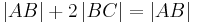
|
(VIII), + 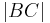
|
| (X) | 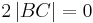
|
(IX), - 
|
| (XI) | Widerspruch, da das zweifache eines Abstands nicht null ergeben kann.
|
--Löwenzahn 17:58, 4. Jun. 2010 (UTC)
= Versuch II ====
Satz in wenn-dann:
- Wenn drei Punkte
 und
und  ein und derselben Gerade g paarweise verschieden sind, dann liegt genau einer zwischen den beiden anderen.
ein und derselben Gerade g paarweise verschieden sind, dann liegt genau einer zwischen den beiden anderen.
- Wenn drei Punkte
Beweis
Es seien also  und
und  drei Punkte.
drei Punkte.
Voraussetzungen:
 und
und  sind Punkte ein und derselben Geraden und paarweise verschieden.
sind Punkte ein und derselben Geraden und paarweise verschieden.
Behauptung
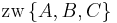 oder
oder 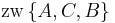 oder
oder 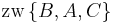
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 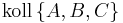
|
Voraussetzung |
| (II) |  und und  paarweise verschieden paarweise verschieden
|
Voraussetzung |
| (III) | (1.)  (2.) 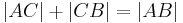 (3.) 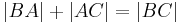
|
I., Axiom II/3 |
| (IV) | (1.)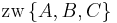 (2.) 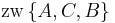 (3.) 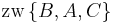
|
III./(1.), III./(2.), III./(3.), Definition (Zwischenrelation) |
| (V) | Behauptung ist wahr |
--Maude001 12:39, 5. Jun. 2010 (UTC)