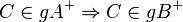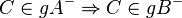Lösung von Aufgabe 8.6 (WS 12 13)
Aus Geometrie-Wiki
Version vom 28. Dezember 2012, 12:19 Uhr von Apfelbaum (Diskussion | Beiträge)
Aufgabe 8.6Es sei Beweisen Sie:
Lösung von User ...--Yellow 17:01, 18. Dez. 2012 (CET) @ yellow Hallöle du hast als zweite Voraussetzung dass a,b,c element von g ist. dass verstehe ich nicht ganz??? Lösung von User ...
|
 eine Gerade der Ebene
eine Gerade der Ebene  . Ferner seien
. Ferner seien  drei nicht kollineare Punkte der Ebene Epsilon. Keiner dieser drei Punkte möge zu
drei nicht kollineare Punkte der Ebene Epsilon. Keiner dieser drei Punkte möge zu 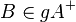 .
.