Lösung von Aufgabe 10.2P (WS 12 13)

Beweisen Sie mit abbildungsgeometrischen Mitteln den Basiswinkelsatz.

Voraussetzung: gleichschenkliges Dreieck mit 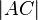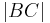$\left| AC \right|$ = $\left| BC \right|$ Behauptung: $\left| Beta \right|$ = $\left| Alpha \right|$

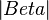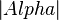
Schritt	Beobachtung
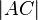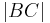
1) $\left| AC \right|$ = $\left| BC \right|$	Vor.
2) m ist Mittelsenkrechte von AB; C $\in$ m	1; Mittelsenkrechtenkriterium
3) Sm (A) = B	2; Def. Geradenspiegelung
4) Sm (C) = C	Def. Fixpunkt
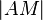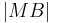
5) $\left| AM \right|$ = $\left| MB \right|$	Def. Mittelsenkrechte
6) Winkel CAM = $\alpha$; Winkel CBM =$\beta$	Def. Winkel
7) Sm ($\alpha$) = $\beta$	5; winkelmaßerhaltung

--Hakunamatata 21:47, 16. Jan. 2013 (CET)

Zwei Anmerkungen dazu:

• Warum folgt aus Schritt 1) C $\in$ m?
• Da du bestimmte Schritte zur Begründung weiterer Schritte nicht verwendet hast, brauchst du sie auch nicht. Oder doch? Für welche Schritte? Bitte ergänzt die Nummern, oder die Schritte können weg gelassen werden.--Tutorin Anne 16:03, 17. Jan. 2013 (CET)

Bei meinem ersten Schritt fehlt etwas ;-) So jetzt ist es ergänzt. Wissen wir nicht, dass der Punkt c Element m ist, dadurch das wir ein gleichschenkliges Dreieck haben?!? --Hakunamatata 17:39, 17. Jan. 2013 (CET)

• Ja richtig. --Tutorin Anne 18:47, 18. Jan. 2013 (CET)

Also passt es jetzt so?? --Hakunamatata 18:09, 19. Jan. 2013 (CET)
Nein, entweder du nutz alle Schritte von 1-6 für irgendwelche Begründungen oder du streichst all die jenigen raus, die du nicht zum Begründen genutzt hast.--Tutorin Anne 12:36, 20. Jan. 2013 (CET)