|
Stufenwinkel, Wechselwinkel, entgegengesetzt liegende Winkel
Zeichnen Sie Bespiele und Gegenbeispiele zu den in der Überschrift genannten Begriffen und laden Sie Ihre Zeichnungen hier mit entsprechenden Kommentaren hoch.
Die Umkehrung des Stufenwinkelsatzes
Satz X.1: (Umkehrung des Stufenwinkelsatzes)
- Es seien
 und und  zwei nicht identische Geraden, die durch eine dritte Gerade zwei nicht identische Geraden, die durch eine dritte Gerade  jeweils geschnitten werden. Es seien ferner jeweils geschnitten werden. Es seien ferner  und und  zwei Stufenwinkel, die bei dem Schnitt von zwei Stufenwinkel, die bei dem Schnitt von  mit mit  und und  entstehen mögen. entstehen mögen.
- Wenn die beiden Stufenwinkel
 und und  kongruent zueinander sind, dann sind die Geraden kongruent zueinander sind, dann sind die Geraden  und und  parallel zueinander. parallel zueinander.
Beweis von Satz X.1: (Umkehrung des Stufenwinkelsatzes)
Es seien 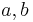 und und  drei paarweise nicht identische Geraden. Die Gerade drei paarweise nicht identische Geraden. Die Gerade  möge möge  in dem Punkt in dem Punkt und die Gerade und die Gerade  in dem Punkt in dem Punkt  schneiden. schneiden.  und und  sei ein Paar von Stufenwinkeln, welches bei dem Schnitt von sei ein Paar von Stufenwinkeln, welches bei dem Schnitt von  und und  mit mit  entstehen möge. entstehen möge.
Voraussetzung:
(i) 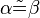
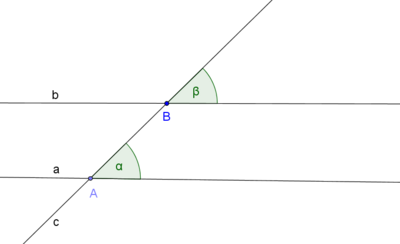
Behauptung:
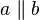
Annahme:
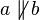
Den Rest können Sie selbst!
Beweisführung Caro44
--Caro44 14:57, 24. Jan. 2013 (CET)
Bemerkung --*m.g.* 17:34, 24. Jan. 2013 (CET)
sehr gut!
Nur für ganz Pingelige: so wie (7) formuliert wurde handelt es sich nicht explizit um eine Gleichung. Hinter (7) verbirgt sich jedoch eine Gleichung: 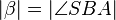 . .
Ok, danke! Stimmt bei Schritt 2 die Begründung Satz I.1 ?--Caro44 20:33, 24. Jan. 2013 (CET)
Hatte ich gar nicht so drauf geachtet. Satz I.1 hilft Ihnen nicht, denn er schließt nicht aus, dass kein Schnittpunkt vorhanden ist.
Sie brauchen aber auch gar keinen Satz: Sie nehmen an, dass die beiden Geraden nicht parallel sind. Nicht parallel sein bedeutet für unsere Gerade nicht keinen Schnittpunkt zu haben, also kurz sie haben einen Schnittpunkt. Formulieren Sie Schritt (2) besser als: Es existiert ein Schnittpunkt der beiden Geraden. Begründung: Sie sind nicht parallel nach (1)
|
 und
und  zwei nicht identische Geraden, die durch eine dritte Gerade
zwei nicht identische Geraden, die durch eine dritte Gerade  jeweils geschnitten werden. Es seien ferner
jeweils geschnitten werden. Es seien ferner  und
und  zwei Stufenwinkel, die bei dem Schnitt von
zwei Stufenwinkel, die bei dem Schnitt von 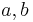 und
und  und die Gerade
und die Gerade  schneiden.
schneiden. 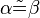

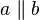
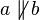

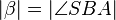 .
.
