Aufgabe 11.03
Es sei  ein Winkel mit den Schenkeln ein Winkel mit den Schenkeln  und und  und dem Scheitel und dem Scheitel  . Ferner sei . Ferner sei  die Winkelhalbierende von die Winkelhalbierende von  , also ein Strahl im Inneren von , also ein Strahl im Inneren von  , der als Anfangspunkt S hat und , der als Anfangspunkt S hat und  in zwei kongruente Teilwinkel in zwei kongruente Teilwinkel 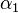 und und 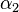 teilt. Auf teilt. Auf  sei ein beliebiger von sei ein beliebiger von  verschiedener Punkt verschiedener Punkt  gegeben. gegeben. 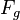 sei der Fußpunkt des Lotes von sei der Fußpunkt des Lotes von  auf auf  : :
Wir konstruieren jetzt auf dem Schenkel  den Punkt den Punkt 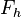 , indem wir auf , indem wir auf  den Abstand den Abstand 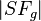 abtragen: abtragen:
Beweisen Sie: 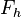 ist der Fußpunkt des Lotes von ist der Fußpunkt des Lotes von  auf auf  . .
Berichtigung der Erstfassung
(Muss es nicht korrekterweise heißen: Beweisen Sie: 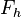 ist der Fußpunkt des Lotes von ist der Fußpunkt des Lotes von  auf auf  ??? --Sweetnightmare5 16:29, 21. Jan. 2013 (CET) ??? --Sweetnightmare5 16:29, 21. Jan. 2013 (CET)
War natürlich ein Fehler, hab's geändert, danke. --*m.g.* 19:34, 21. Jan. 2013 (CET))
Anfrage Sallie Field
Dürfen wir bei diesem Beweis die euklidische Geometrie anwenden und einfach über die Innenwinkelsumme im Dreieck gehen?
Warum wollen Sie das tun? Es geht problemlos mit den Mitteln der absoluten Geometrie. Die Verwendung der Innenwinkelsumme würde die Sache nur komplizierter machen. --*m.g.* 11:25, 23. Jan. 2013 (CET)
Lösung User ...

--B..... 16:45, 24. Jan. 2013 (CET)--B..... 00:52, 24. Jan. 2013 (CET)
Kommentar --*m.g.* 10:01, 25. Jan. 2013 (CET)
- Schritt (2) Begründung: Laut Konstruktion von
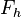 . Dass wir . Dass wir 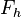 überhaupt so konstruieren können ist durch Ihre weiteren Begründungen gewährleistet. Solche Begründungen schiebt man besser vor die Beweistabelle. Da ich diese Konstruktion vorgegeben habe, brauchen Sie die Durchführbarkeit nicht zu begründen. (Als Fehler würde ich Ihnen die entsprechende Begründung auf keinen Fall ankreiden.) überhaupt so konstruieren können ist durch Ihre weiteren Begründungen gewährleistet. Solche Begründungen schiebt man besser vor die Beweistabelle. Da ich diese Konstruktion vorgegeben habe, brauchen Sie die Durchführbarkeit nicht zu begründen. (Als Fehler würde ich Ihnen die entsprechende Begründung auf keinen Fall ankreiden.)
- Schritt (6) ist nicht sauber begründet. Sie sollen zeigen:
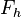 ist der Fußpunkt des Lotes von ist der Fußpunkt des Lotes von  auf auf  . Anders ausgedrückt: Sie sollen zeigen, dass . Anders ausgedrückt: Sie sollen zeigen, dass 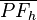 das Lot von das Lot von  auf auf  ist. Die Def. Lot bzw. Def. senkrecht geben uns Kriterien an, nach denen wir entscheiden können, ob die Behauptung erfüllt ist. Es bleibt aber vor allem zu zeigen dass die Kriterien erfüllt sind. Sie müssen also begründen, dass ist. Die Def. Lot bzw. Def. senkrecht geben uns Kriterien an, nach denen wir entscheiden können, ob die Behauptung erfüllt ist. Es bleibt aber vor allem zu zeigen dass die Kriterien erfüllt sind. Sie müssen also begründen, dass 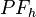 senkrecht auf senkrecht auf  steht. Tipp: Weil nach Voraussetzung steht. Tipp: Weil nach Voraussetzung 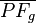 das Lot von das Lot von  auf auf  ist, muss ist, muss 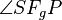 ein Rechter sein ... . ein Rechter sein ... .
Frage
Irgendwie stimmt doch etwas in der Aufgabenstellung nicht oder??
--Hauleri 13:05, 26. Jan. 2013 (CET)
|
 ein Winkel mit den Schenkeln
ein Winkel mit den Schenkeln  und
und  und dem Scheitel
und dem Scheitel  . Ferner sei
. Ferner sei  die Winkelhalbierende von
die Winkelhalbierende von 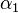 und
und 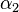 teilt. Auf
teilt. Auf  gegeben.
gegeben. 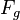 sei der Fußpunkt des Lotes von
sei der Fußpunkt des Lotes von 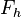 , indem wir auf
, indem wir auf 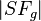 abtragen:
abtragen:

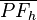 das Lot von
das Lot von 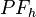 senkrecht auf
senkrecht auf 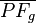 das Lot von
das Lot von 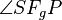 ein Rechter sein ... .
ein Rechter sein ... .

