Lösung von Aufgabe 12.03 WS 12 13
Aufgabe 12.03In der vorangegangenen Übungsserie haben wir zwei Aufgaben zu Winkelhalbierenden gelöst. Diese Aufgaben bilden die Grundlage für ein Winkelhalbierendenkriterium. Ergänzen Sie dieses: Lösung User ...Pg den selben Abstand zu Ph hat. g und h sein die Schenkel des Winkels. --Yellow 21:21, 26. Jan. 2013 (CET)
... wenn die Winkelhalbierende den selben Abstand zu den Schenkeln von alpha hat. Lösung User ... |
 , wenn ...
, wenn ...
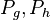 aus den Übungsaufgaben. Es waren die Fußpunkte der Lote von
aus den Übungsaufgaben. Es waren die Fußpunkte der Lote von  auf die Schenkel des Winkels. Die Länge der Lote von P auf die Schenkel ist jeweils der .... von P zu den Schenkeln.--
auf die Schenkel des Winkels. Die Länge der Lote von P auf die Schenkel ist jeweils der .... von P zu den Schenkeln.--
