Beziehungen zwischen Seitenlängen und Innenwinkelgrößen von Dreiecken WS 12 13
Inhaltsverzeichnis |
Satz XIV.1: (Der größeren Seite liegt der größere Winkel gegenüber)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen.
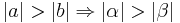
- Es sei
Beweis von Satz XIV.1
Es sei  ein Dreieck.
ein Dreieck.
Voraussetzung:
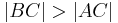 bzw.
bzw. 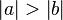
Behauptung:
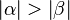
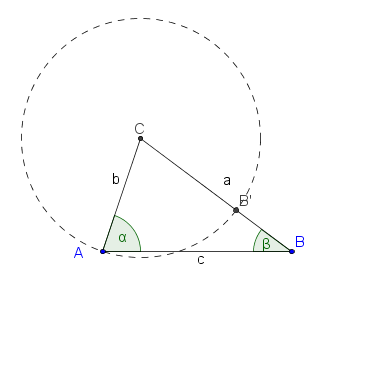
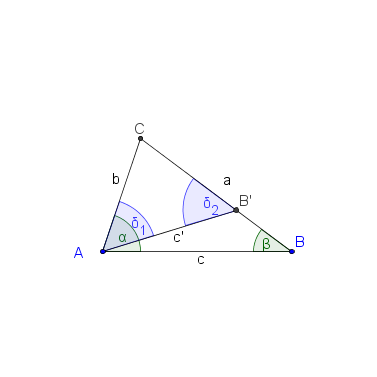
Die folgenden Hilfskonstruktionen liefern die Beweisidee (kommentieren Sie die Abbildungen und führen Sie den Beweis):

--TobiWan 00:25, 29. Jan. 2013 (CET)
Also im Grunde denke ich das der Ansatz auf jeden fall richtig ist! Ich habe es auch mal versucht... meine ersten vier Schritte entsprechen deiner vorgehensweise.
Dann:
4. 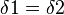 Begründung: deine 4; Basiswinkelsatz
Begründung: deine 4; Basiswinkelsatz
5. 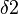 ist Außenwinkel von
ist Außenwinkel von  im Dreieck ABB` Begründung: Def. Außenwinkel
im Dreieck ABB` Begründung: Def. Außenwinkel
6. Abstand von  =
= 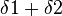 Begründung: Mein 4. Schritt
Begründung: Mein 4. Schritt
7. Abstand 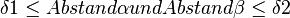 Begründung: 6. , schwacher Außenwinkelsatz
Begründung: 6. , schwacher Außenwinkelsatz
8. 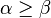 Begründung: 4,6,7--Hakunamatata 17:03, 29. Jan. 2013 (CET)
Begründung: 4,6,7--Hakunamatata 17:03, 29. Jan. 2013 (CET)
Satz XIV.2: (Dem größeren Winkel liegt die größere Seite gegenüber)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen. 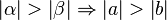
- Es sei
Beweis von Satz XIV.2
Zusatzaufaufgabe
Hier ist der Link zu meinem Beweis:
http://wikis.zum.de/geowiki/Datei:2013-01-29_17.06.06.jpg--Hakunamatata 17:09, 29. Jan. 2013 (CET)