Lösung von Zusatzaufgabe 12.4P (WS 12 13)

Beweisen Sie den schwachen Außenwinkelsatz. Hinweis: Sie dürfen sich auf Aufgabe 12.3 beziehen.

--TobiWan 23:16, 30. Jan. 2013 (CET)
Super - toll, dass du deinen Beweis einstellst.
Dein Ansatz ist völlig richtig. Wie kommst du auf Schritt 3? Warum folgt er aus Schritt 1 und 2 - was hast du da wie verrechnet?--Tutorin Anne 17:15, 31. Jan. 2013 (CET)

Wir könne hier eigentlich 2 Fälle betrachten.
Fall 1: 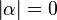$\left| \alpha \right| = 0$, dann muss gelten: 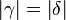$\left| \gamma \right| =\left| \delta \right|$ Problem: Wenn ein Innenwinkel das Maß 0 hat, entsteht kein Dreieck.
-> Fall 1 ist zu verwerfen.

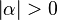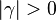Fall2: $\left| \alpha \right| > 0$ und $\left| \gamma \right| > 0$  ; Es entsteht ein Dreieck.
Dann kann auch keiner der beiden Winkel das gleiche Maß wie $\delta$ haben. Dass sie nicht größer als dieser sein können, versteht sich von selbst. Daraus folgt dann, dass beide Winkel jeweils kleiner sein müssen als $\delta$.
Meintest du das Anne?
--TobiWan 00:55, 3. Feb. 2013 (CET)

Nein, das meine ich eigentlich nicht. Da wir ein Dreieck voraussetzen, brauchst du Fall 1 nicht betrachten.
Ich bin der Meinung, dass du Schritt 2 überhaupt nicht brauchst.--Tutorin Anne 07:20, 4. Feb. 2013 (CET)

Okay, stimmt eigentlich....Wenn ich in 1.) sage, dass die Summe der Winkel Delta ergibt, folgt daraus direkt, dass die alpha und gamma kleiner sein müssen.--TobiWan 19:35, 4. Feb. 2013 (CET)

• Eben, aber die Frage ist trotzdem, warum genau? (Hinweis: Die Gleichung 4 + x =2 lässt sich ja auch lösen und 4 ist deshalb nicht kleiner 2.)--Tutorin Anne 16:10, 5. Feb. 2013 (CET)

Laut Definition "Winkelmaß", kann jeder Winkel nur eine reele Zahl zwischen 0 und 180 zugeordnet werden, heißt kleiner Null geht nicht. Und wir wissen ein Winkel im Dreieck kann nicht das Maß 0 haben, denn sonst gäbe es kein Dreieck.--TobiWan 11:26, 6. Feb. 2013 (CET)

• Genau so ist es!--Tutorin Anne 13:59, 6. Feb. 2013 (CET)