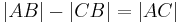Lösung von Aufgabe 6.9
Inhaltsverzeichnis |
Vorlage
Satz:
- Von drei paarweise verschiedenen Punkten
 und
und  ein und derselben Geraden
ein und derselben Geraden  liegt genau einer zwischen den beiden anderen.
liegt genau einer zwischen den beiden anderen.
- Von drei paarweise verschiedenen Punkten
Beweisen Sie diesen Satz.
Lösung --Schnirch 13:50, 16. Jun. 2010 (UTC)
Satz in wenn-dann:
- Wenn drei Punkte
 und
und  kollinear sind, dann liegt genau einer zwischen den beiden anderen Punkten.
kollinear sind, dann liegt genau einer zwischen den beiden anderen Punkten.
- Wenn drei Punkte
Beweis
Es seien also  und
und  drei Punkte.
drei Punkte.
Voraussetzungen:
koll( und
und  )
)
Behauptung
- es gilt genau eine der drei möglichen Zwischenrelationen:
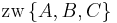 oder
oder 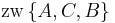 oder
oder 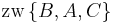
- es gilt genau eine der drei möglichen Zwischenrelationen:
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 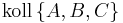
|
Voraussetzung |
| (II) | es gilt eine der drei Gleichungen:
|
(I), Axiom II/3 |
| (III) | 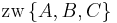 oder oder 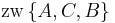 oder oder 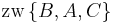
|
(II), Def (Zwischenrelation) |
| (IV) | zu zeigen: es liegt genau einer zwischen den beiden anderen
| |
| (V) | 
|
(IV), (Axiom II/3) |
| (VI) | 
|
rechnen mit reellen Zahlen, (Axiom II/2) |
| (VII) | 
|
(VI gleichgesetzt), rechnen mit reellen Zahlen |
| (VIII) | 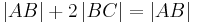
|
(VII), + 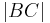
|
| (IX) | 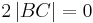
|
(VIII), - 
|
| (X) | Widerspruch, da die beiden Punkte B und C identisch sein müssten, nach Voraussetzung aber drei verschiedene Punkte A, B und C gegeben sind.
|
Eine Frage: Wenn im Satz von drei PAARWEISE VERSCHIEDENEN Punkten die Rede ist, warum lassen sie es einfach weg? Ich werde immer unsicherer was diese Spitzfindigkeiten angeht, weil nie die gleichen Regeln zu gelten scheinen und mich das ganz verrückt macht! Darf ich davon ausgehen, das wenn von drei Punkte die Rede ist, diese immer verschieden sind oder nicht? Wenn ja wieso darf ich das in diesem Fall und in anderen nicht? Wenn ich nicht davon ausgehen kann, muss das "paarweise verschieden" dabei sein, weil die Voraussetzung sonst eine ganz andere ist??? --Principella 15:45, 21. Jun. 2010 (UTC)
vorausgegangene Diskussion
Versuch I
Satz:
- Von drei paarweise verschiedenen Punkten
 und
und  ein und derselben Geraden
ein und derselben Geraden  liegt genau einer zwischen den beiden anderen.
liegt genau einer zwischen den beiden anderen.
- Von drei paarweise verschiedenen Punkten
Beweisen Sie diesen Satz.
Satz in wenn-dann:
- Wenn drei Punkte
 und
und  kollinear sind, dann liegt genau einer zwischen den beiden anderen Punkten (und umgekehrt???) .
kollinear sind, dann liegt genau einer zwischen den beiden anderen Punkten (und umgekehrt???) .
- Wenn drei Punkte
Beweis
Es seien also  und
und  drei Punkte.
drei Punkte.
Voraussetzungen:
koll( und
und  )
)
Behauptung
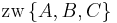 oder
oder 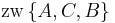 oder
oder 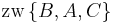
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 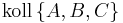
|
Voraussetzung |
| (II) | Für drei beliebige Punkte  und und  gilt: gilt: 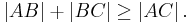
|
Axiom II/3: (Dreiecksungleichung) |
| (III) | 
|
Axiom II/3.1
|
| (IV) | ||
| (V) |
...und jetzt? --Heinzvaneugen
Ich glaube, es ist noch zu zeigen, dass genau einer zwischen den beiden anderen liegt. Habe deinen Beweis ab Schritt IV weitergeführt:
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (IV) | 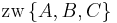 oder oder 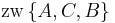 oder oder 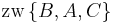
|
Def (Zwischenrelation) |
| (V) | zu zeigen: es liegt genau einer zwischen den beiden anderen
| |
| (VI) | 
|
(Axiom II/3) |
| (VII) | 
|
rechnen mit reellen Zahlen, (Axiom II/2) |
| (VIII) | 
|
(VII gleichgesetzt), rechnen mit reellen Zahlen |
| (IX) | 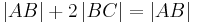
|
(VIII), + 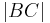
|
| (X) | 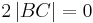
|
(IX), - 
|
| (XI) | Widerspruch, da das zweifache eines Abstands nicht null ergeben kann.
|
--Löwenzahn 17:58, 4. Jun. 2010 (UTC)
= Versuch II ====
Satz in wenn-dann:
- Wenn drei Punkte
 und
und  ein und derselben Gerade g paarweise verschieden sind, dann liegt genau einer zwischen den beiden anderen.
ein und derselben Gerade g paarweise verschieden sind, dann liegt genau einer zwischen den beiden anderen.
- Wenn drei Punkte
Beweis
Es seien also  und
und  drei Punkte.
drei Punkte.
Voraussetzungen:
 und
und  sind Punkte ein und derselben Geraden und paarweise verschieden.
sind Punkte ein und derselben Geraden und paarweise verschieden.
Behauptung
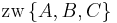 oder
oder 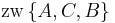 oder
oder 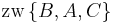
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 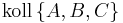
|
Voraussetzung |
| (II) |  und und  paarweise verschieden paarweise verschieden
|
Voraussetzung |
| (III) | (1.)  (2.) 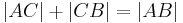 (3.) 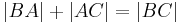
|
I., Axiom II/3 |
| (IV) | (1.)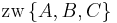 (2.) 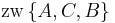 (3.) 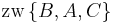
|
III./(1.), III./(2.), III./(3.), Definition (Zwischenrelation) |
| (V) | Behauptung ist wahr |
--Maude001 12:39, 5. Jun. 2010 (UTC)