Bresenham-Algorithmus (in Arbeit)
Inhaltsverzeichnis |
Allgemeines zum Bresenham Algorithmus
Motivation des Algorithmus
Der Bresenham Algorihtmus, ist ein Verfahren um Geraden möglichst "gut" auf Anzeigegeräten zu zeichnen. Hier heisst "gut", dass die Abweichung zwischen dem gezeichneten und dem gedachten Objekt möglichst gering ist.
Das Problem beim Darstellen einer Strecke auf einem Anzeigegerät ist, dass das erzeugte Bild nur durch endlich viele Punkte aufgebaut ist, dadurch entstehen "Lücken" beim Zeichnen. Da unsere Augen nur eine endliche Auflösung verarbeiten können, scheint uns ein Bild auf dem Monitor nicht durch einzelne Punkte aufgebaut zu sein, sondern es entstehen für uns geometrische Formen, die wir mit unserer Vorstellung von mathematischen Objekten in Einklang bringen können.
Eine Gerade wie wir sie auf dem Bildschirm wahrnehmen.
Gerade in normaler Größe
Hier sieht man dieselbe Gerade um das Achtfache vergrößert.
Gerade bis auf die Pixeleben vergrößert
Effektivität des Algorithmus
Dieser Algorithmus ist auch in heutiger Zeit in seiner Geschwindigkeit und Einfachheit ungeschlagen, da sich die Rechenoperationen h auf Addition und die Multiplikation mit Zwei beschränken. Dadurch kann dieser Rechenalgorithmus direkt in die Hardware der Grafikkarten implementiert werden.
Potenzen:
Obwohl in den Rechentermen Potenzen auftreten, kann man diese umgehen.
Hierfür betrachten wir den Ausdruck:
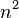
die zweite Binomische Formel liefert:
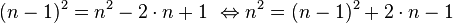
durch rekursives Anwenden dieser Formel lassen sich Potenzen solange vereinfachen bis die Basis Eins erreicht ist und damit die Potenz verschwindet.
Multiplikation mit Zwei:
Eine Multiplikation mit Zwei ist für einen Computer eine elementare Rechenoperation, da die sogenannte Shift Operation (Verrückungsoperation) durchgeführt wird.
Wir erinnern uns an die Darstellung von Zahlen im Binärsystem.
| Wertigkeit der Stelle | 2^7 = 128 | 2^6 = 64 | 2^5 = 32 | 2^4 = 16 | 2^3 = 8 | 2^2 = 4 | 2^1 = 2 | 2^0 = 1 |
|---|---|---|---|---|---|---|---|---|
| Binärzahl | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
Hier wird die Zahl (im Dezimalsystem) dargestellt
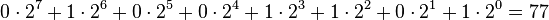
Multiplizerien wir nun mit Zwei, so folgt:
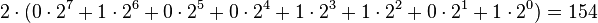

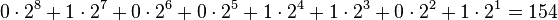
Also die Zahl 154 (Dezimal) in Binärdarstellung:
| Wertigkeit der Stelle | 2^7 = 128 | 2^6 = 64 | 2^5 = 32 | 2^4 = 16 | 2^3 = 8 | 2^2 = 4 | 2^1 = 2 | 2^0 = 1 |
|---|---|---|---|---|---|---|---|---|
| Binärzahl | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
Vergleichen wir nun die Darstellung der Zahl 77 mit der Darstellung der Zahl 154, so fällt auf, dass durch die Multiplikation mit Zwei, jedes Bit um eine Stelle nach links verschoben wurde.
Bresenham-Algortihmus für Geraden
Algorithmus für Gerade mit der Steigung m <= 1
Betrachten wir die folgende Problemstellung: Wir wollen eine Gerade, welche in Hesseform gegeben ist, mit einem Plotter (z.B. auf einem Monitor) zeichnen lassen. Wir wollen für den ersten Teil nur Geraden mit einer Steigung 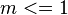 betrachten.
betrachten.
Sei die Gerade 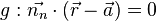 gegeben. Hierbei ist
gegeben. Hierbei ist 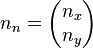 der normierte Normalenvektor,
der normierte Normalenvektor, 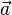 ein gegebener Ortsvektor eines Punktes der Geraden.
ein gegebener Ortsvektor eines Punktes der Geraden.
Wir geben den Startpunkt der Geraden auf unserem Plotter die Koordinaten (0,0), d.h. jede Gerade, die wir zeichnen erhält damit ein eigenes Koordinatensystem.
Der erste Punkt den wir zeichnen ist natürlich der Punkt 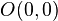 , denn dies haben wir so festgelegt. Nun müssen wir für den nächsten Punkt entscheiden, ob wir nur ein Pixel (allgemein: einen Plotterschritt) nach rechts zum Punkt
, denn dies haben wir so festgelegt. Nun müssen wir für den nächsten Punkt entscheiden, ob wir nur ein Pixel (allgemein: einen Plotterschritt) nach rechts zum Punkt  gehen oder ein Pixel nach rechts und nach oben zum Punkt
gehen oder ein Pixel nach rechts und nach oben zum Punkt  . Um dies zu entscheiden müssen wir die Abstände, die die jeweiligen Punkte zu der idealen Geraden haben, vergleichen. Der Punkt mit dem kleineren Abstand wird dann angesteuert.
. Um dies zu entscheiden müssen wir die Abstände, die die jeweiligen Punkte zu der idealen Geraden haben, vergleichen. Der Punkt mit dem kleineren Abstand wird dann angesteuert.
Hierfür betrachten wir die Differenz der Abstände 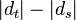 .
.
Da wir nur die y-Achsenabweichung der gezeichneten Geraden mit dem Auge wahrnehmen, aber der folgende Zusammenhang besteht, können wir mit den reinen Abständen, die wir aus der Hesseform gewinnen rechnen:
zu zeigen ist: 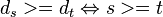
es gilt:
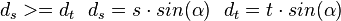
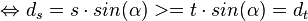
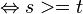
Nun gehen wir nicht mehr von dem ersten Punkt (Ursprung) 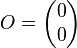 aus, sondern von einem allgemeinen Punkt
aus, sondern von einem allgemeinen Punkt 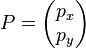 , dementsprechend lautet dann der Punkt
, dementsprechend lautet dann der Punkt
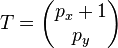 und der Punkt
und der Punkt 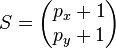
Achtung:
Wie wir unter dem Abschnitt Hesseform gesehen haben, kommt es bei dem Vorzeichen der Abständen der Punkte auf die Lage der Punkte im Bezug zur Geraden und dem Ursprung an. Da der Punkt  nicht zwischen Gerade und Ursprung liegt, ist der Abstand
nicht zwischen Gerade und Ursprung liegt, ist der Abstand 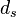 positiv, analog ist der Abstand
positiv, analog ist der Abstand 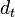 negativ.
negativ.
Also folgt mit:
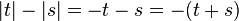
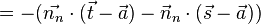
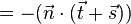
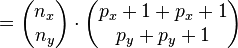
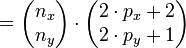
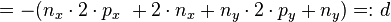
Nun entscheidet das Vorzeichen von  welcher Punkt angesteuert wird:
welcher Punkt angesteuert wird:
Für 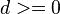 der Punkt
der Punkt 
Für 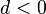 der Punkt
der Punkt 
Algorithmus für Gerade mit der Steigung m > 1
Wir wollen nun den Fall für Geraden betrachten deren Steigung größer ist als Eins. Die Vorausetzungen seien wie in dem Fall für die Steigung kleiner Eins. Im Fall der Steigung kleiner gleich Eins musste die Stiftposition bei jedem Zeichenschritt in x-Achsenrichtung inkrementiert werden und es wurde anhand einer Gleichung entschieden ob wir auch in y-Richtung inkrementieren müssen. Im Falle der Steigung größer Eins ist es nun genau umgekehrt, wir müssen bei jedem Zeichenschritt in y-Richtung inkrementieren und an Hand der Abstandsgleichung entscheiden ob wir dies auch in x-Richtung tun müssen.
Wir betrachten wieder die Differenz der Abstände:
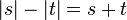
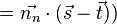
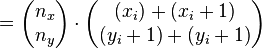
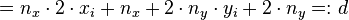
Auch hier entscheidet nun wieder die Differenz  welcher Punkt angesteuert werden soll.
welcher Punkt angesteuert werden soll.
Für 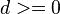 wird der Punkt
wird der Punkt 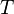 angesteuert.
angesteuert.
Für 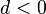 wird der Punkt
wird der Punkt  angesteuert.
angesteuert.
Zusammenfassung
Durch die beiden Fallunterscheidungen in 2.1 und 2.2 kann nun im ersten Quadranten jede Linie mit positiver Steigung gezeichnet werden. Wollen wir nun in der Lage sein, auch die negativen Steigungen zu zulassen, Spiegeln wir den Endpunkt der Strecke in den ersten Quadranten, indem wir in die passende Gleichung die Absolutbeträge des Punktes und des Normalenvektors einsetzten.
Also für Steigungen mit 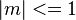
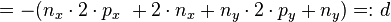
Also für Steigungen mit 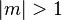
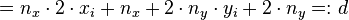
Literaturnachweise
Olaf Müller, Ralf Kunze, Vorlesungskript SS 2002: Computergrafik, http://www-lehre.inf.uos.de/~cg/2002/skript/node30.html 11.03.2012
J. Frank, Informatik, http://www.wvs.be.schule.de/faecher/informatik/material/grafik/strecke3.html 11.03.2012
Markus Grodd, Der Bresenham-Algorithmus, http://algorithm.name/rasteralgorithmus_1.html, 11.03.2012

