Übungen 01

Aufgabe 1

Beschreibt folgende Gleichung einen Kreis? Bestimmen Sie Mittelpunkt und Radius.
a) 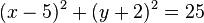$(x-5)^2+(y+2)^2=25$
b)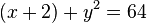$(x+2)+y^2=64$
c)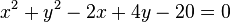$x^2+y^2-2x+4y-20=0$
d)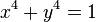$x^4+y^4=1$
e)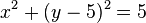$x^2+(y-5)^2=5$
f)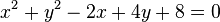$x^2+y^2-2x+4y+8=0$

Aufgabe 2

Bestimmen Sie die Kreisgleichung folgender Kreise, wobei M immer der Mittelpunkt ist:
a) M(0|0) r=3
b) M(6|-8) und P(0|0) $\in$ k
c) A(3|2) und B(-1|6) liegen sich diametral gegenüber (d.h. Ende des Durchmessers)
d) A(1|-2), B(3|0), C(5|-2) liegen auf dem Kreis

Lösungen_Übungen01