Übungen 02
Aus Geometrie-Wiki
Version vom 30. April 2013, 13:01 Uhr von Cplicht (Diskussion | Beiträge)
Aufgabe 1
Es seien 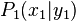 und
und 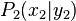 zwei beliebige voneinander verschiedene Punkte einer Geraden mit der Gleichung
zwei beliebige voneinander verschiedene Punkte einer Geraden mit der Gleichung
 (a,b,c
(a,b,c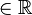 ,
, 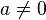 oder
oder 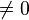 ).
).
Zeigen Sie, das gilt:
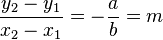
Aufgabe 2
Stellen Sie Gleichungen in der Form ax+by=c und der y=mx+n der Geraden durch die gegebenen Punkte auf
a) 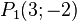 und
und 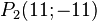
b)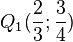 und
und 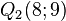
Aufgabe 3
Begründen Sie, dass die Zweipunkteform 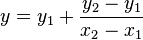 für eine Gerade
für eine Gerade  gilt mit
gilt mit 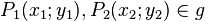 . (Tipp: Aufgabe 1)
. (Tipp: Aufgabe 1)

