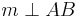Mittelsenkrechte und Winkelhalbierende
Aus Geometrie-Wiki
Version vom 24. Juni 2010, 21:54 Uhr von *m.g.* (Diskussion | Beiträge)
Inhaltsverzeichnis |
Mittelsenkrechte und Winkelhalbierende
Mittelsenkrechte
Eine Mittelsenkrechte ist das, was ihre Bezeichnung ausdrückt: eine Gerade, die eine Strecke halbiert und senkrecht auf ihr steht.
Definition VI.1: (Mittelsenkrechte)
- Es sei
 eine Gerade und
eine Gerade und  eine Strecke, die durch
eine Strecke, die durch  im Punkt
im Punkt  geschnitten wird.
geschnitten wird.  ist die Mittelsenkrechte von
ist die Mittelsenkrechte von  , wenn
, wenn
- Es sei
Satz VI.1: (Existenz und Eindeutigkeit der Mittelsenkrechten)
- Jede Strecke hat in jeder Ebene, zu der die Strecke vollständig gehört, genau eine Mittelsenkrechte.
Beweis von Satz VI.1
Es sei  eine Strecke, die vollständig zur Ebene
eine Strecke, die vollständig zur Ebene  gehören möge.
gehören möge.
Behauptungen:
- Es gibt in
 genau Gerade Fehler beim Parsen(Unbekannte Funktion „\m“): \ \m
genau Gerade Fehler beim Parsen(Unbekannte Funktion „\m“): \ \m
, die die Mittelsenkrechte von  ist
ist
- Element 2
- Element 3