Lösung von Aufgabe 6.04 S SoSe 13
Aus Geometrie-Wiki
Version vom 3. Juni 2013, 21:49 Uhr von *m.g.* (Diskussion | Beiträge)
Aufgabe 6.04Es seien Begründen Sie, warum die Zerlegung einer Geraden
Lösung User ...Lösung User ...Lösung User ...
|
 eine Menge und
eine Menge und 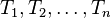 Teilmengen von
Teilmengen von 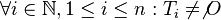
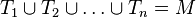
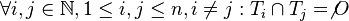
 in die Halbgeraden
in die Halbgeraden  und
und  keine Klasseneinteilung von
keine Klasseneinteilung von 
