Übungen 06
Aus Geometrie-Wiki
Version vom 11. Juni 2013, 15:33 Uhr von Cplicht (Diskussion | Beiträge)
Inhaltsverzeichnis |
Aufgabe 1
Gegeben sind ein Unterraum 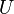 eines Vektorraums
eines Vektorraums 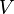 und Vektoren
und Vektoren 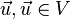 .
.
Welche der Aussagen sind richtig? Geben Sie Begrünudngen oder Gegenbeispiele an.
a) Gehören 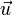 und
und 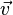 nicht zu
nicht zu 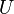 , so ist auch
, so ist auch 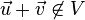 .
.
b) Gehören 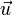 und
und 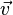 nicht zu
nicht zu 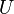 , so ist auch
, so ist auch 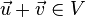 .
.
c) Gehört 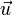 zu U, nicht aber
zu U, nicht aber 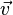 , so ist
, so ist 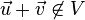 .
.
Aufgabe 2
Geben Sie bei folgenden Teilmengen des Vektorraums 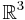 an, ob Sie Unterräume sind; begründen Sie Ihre Aussagen!
an, ob Sie Unterräume sind; begründen Sie Ihre Aussagen!
a) 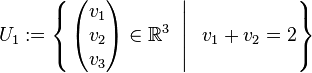
b) 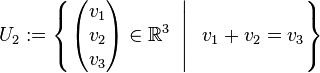
c) 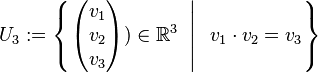
Aufgabe 3
Begründen Sie, dass Lösungsmengen inhomogener Gleichungssysteme keine Unterräume sind.
Aufgabe 4
Weisen Sie nach, dass die Menge aller 2x2 Matrizen der Form 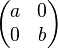 mir
mir 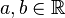 und den in der Vorlesung verwendeten Verknüpfungen
und den in der Vorlesung verwendeten Verknüpfungen  und
und  ein Unterraum aller Matrizen der Form
ein Unterraum aller Matrizen der Form 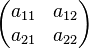 ist.
ist.

