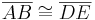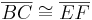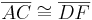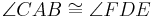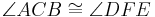Dreieckskongruenz
Aus Geometrie-Wiki
Version vom 27. Juni 2010, 17:29 Uhr von *m.g.* (Diskussion | Beiträge)
Inhaltsverzeichnis |
Die beiden grundlegenden Ideen der Kongruenz
Bewegungsgeometrie
naive Deckungsgleichheit
Bewegungen: abstandserhaltende Abbildungen der Ebene auf sich
Euklid lässt grüßen: Dreieckskongruenz
Streckenkongruenz
Wir erinnern uns an die Diskussion zu Anfang des Semesters.
Die Auswertung des Quiz zeigt: Alle drei Aussagen sind synonym.
Momentan jedoch eigentlich noch nicht. Uns fehlt eine Definition des Begriffs der Streckenkongruenz.
Definition VII.1: (Streckenkongruenz)
- Zwei Strecken sind kongruent, wenn sie dieselbe Länge haben.
- In Zeichen
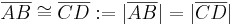
- Zwei Strecken sind kongruent, wenn sie dieselbe Länge haben.
Winkelkongruenz
Analog zum Begriff der Streckenkongruenz sollen zwei Winkel genau dann kongruent zueinander genannt werden, wenn sie dieselbe Größe haben.
Definition VII.2 : (Winkelkongruenz)
- Zwei Winkel die dieselbe Größe haben heißen kongruent zueinander.
- In Zeichen:
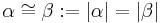
- Zwei Winkel die dieselbe Größe haben heißen kongruent zueinander.
Dreieckskongruenz
In der Schule spricht man häufig davon, dass zwei Dreiecke dann kongruent zueinander sind, wenn sie in allen Stücken übereinstimmen. Unter den Stücken eines Dreieck sind dabei die jeweils drei Seiten und die jeweils drei Innenwinkel zu verstehen.
Definition VII.3: (Dreieckskongruenz)
- Wenn für zwei Dreiecke
 und
und  die folgenden Kongruenzen gelten
die folgenden Kongruenzen gelten
- Wenn für zwei Dreiecke