Lösung von Aufgabe 11.09 SoSe 13
Lösung IIIu13
Gegeben seien der Winkel 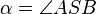 , die Winkelhalbierende w von
, die Winkelhalbierende w von  und der Punkt P mit
und der Punkt P mit 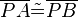
z.z.: P  w
w
Beweis:
1) 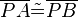 ; (>Voraussetzung)
; (>Voraussetzung)
2) 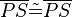 ; (>trivial)
; (>trivial)
3) Sei m die Mittelsenkrechte von  und M der Mittelpunkt von
und M der Mittelpunkt von  ; (>Existenz der Mittelsenkrechten)
; (>Existenz der Mittelsenkrechten)
4) 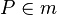 ; (>Def. Mittelsenkrechte, (1))
; (>Def. Mittelsenkrechte, (1))
5) 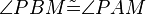 ; (>(1),Basiswinkelsatz)
; (>(1),Basiswinkelsatz)
6) 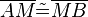 ; (>(3))
; (>(3))
7) 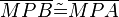 ; (>(1),(5),(6),sws)
; (>(1),(5),(6),sws)
8) 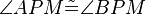 ; (>(7))
; (>(7))
9) 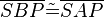 ; (>(1),(8),(2),sws)
; (>(1),(8),(2),sws)
10) 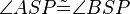 ; (>(9))
; (>(9))
11) 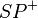 ist die Winkelhalbierende w; (>(10), Def. und Eindeutigkeit der Winkelhalbierenden)
ist die Winkelhalbierende w; (>(10), Def. und Eindeutigkeit der Winkelhalbierenden)
12) 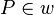 ; (>(11))
; (>(11))
Muss ich hier explizit sagen, dass P im Inneren vom Winkel liegt? Darf ich das voraussetzen oder muss ich eine Fallunterscheidung machen?
--Illu13 23:02, 10. Jul. 2013 (CEST)
Bemerkung --*m.g.* 10:12, 11. Jul. 2013 (CEST)
Wir gehen davon aus, das  zu den Schenkeln von
zu den Schenkeln von 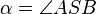 ein und denselben Abstand hat. Das bedeutet nicht, dass
ein und denselben Abstand hat. Das bedeutet nicht, dass 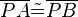 gilt.
gilt.

