| (1) Ein gemeines Dreiecksknux ist eine Gerade 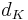 , zu der ein Dreieck , zu der ein Dreieck  derart existiert, dass keiner der Eckpunkte von derart existiert, dass keiner der Eckpunkte von  zu zu 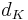 gehört, aber jede Seite des Dreiecks gehört, aber jede Seite des Dreiecks  genau einen Punkt mit genau einen Punkt mit 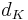 gemeinsam hat. gemeinsam hat. |
| → | Natürlich gibt es keine Dreiecksknuxe, es bleibt uns aber unbenommen, über den Begriff des Dreiecksknuxes auf extravante Weise den Begriff der leeren Menge noch einmal zu definieren. Merke: Ob es Repräsentanten für einen definierten Begriff B gibt oder nicht, ist völlig irrelevant bezüglich einer Entscheidung, ob es sich bei der Definition von B um eine solche handelt oder nicht. |
| (2) Der gemeine Dreiecksknux ist die Gerade, die alle drei Seiten eines Dreicks schneidet und dabei nicht durch die Eckpunkte dieses Dreiecks geht. |
| → | Vorsicht ist angemahnt, wenn der bestimmte Artikel in einer Definition verwendet wird. Im vorliegenden Fall ist es egal. Es gibt keinen gemeinen Drteiecksknux. Die Definition ist also völlig korrekt und im übrigen äquivalent zu (1). (In beiden Fällen wird die leere Menge definiert.) |
| (3) Es sei  ein Dreieck. Der gemeine Dreiecksknux von ein Dreieck. Der gemeine Dreiecksknux von  ist der Kreis ist der Kreis  , der jede Seite von , der jede Seite von  in genau einem Punkt berührt. in genau einem Punkt berührt. |
| → | Ja, ja der gemeine Dreiecksknux formerly known as "Inkreis". Saubere Definition, es bleibt uns unbenommen, eine Umbenennung vorzunehmen. Dass wir damit in der Mathematik-Community viel Beifall ernten werden, ist eher nicht zu erwarten, aber verbieten dürfen sie uns die Umbenennung nicht. Merke: Mathematik ist zutiefst basisdemokratisch. Ergo: Wer Definitionen auswendig lernt, ist kein guter Demokrat. |
| (4) Wenn zu einem Dreieck ein Dreiecksknux entsprechend (3) existiert, so ist das Dreieck ein Tangentendreieck. |
| → | Saubere Definition trotzdem ziemlich sinnlos. Jedes Dreieck wäre damit ein Tangentendreieck. Damit macht es nicht viel Sinn, den Begriff zu definieren. |