Aufgabe 12.04
Die Gerade  sei Tangente an den Kreis sei Tangente an den Kreis  (Mittelpunkt (Mittelpunkt  ) im Punkt ) im Punkt  . Beweisen Sie: . Beweisen Sie: 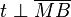 . .
Lösung
Annahme:
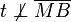 . .
Nach der Existenz des Lotes von  auf auf  muss es jetzt eine Strecke muss es jetzt eine Strecke 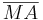 geben, die das Lot von geben, die das Lot von  auf auf  ist. Selbstverständlich ist ist. Selbstverständlich ist  verschieden von verschieden von  , da ansonsten , da ansonsten 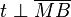 gelten würde. Weil gelten würde. Weil  Tangente an Tangente an  ist, kann ist, kann  nicht zu nicht zu  gehören. gehören.
Fall 1:
 liegt außerhalb von liegt außerhalb von  . Der Abstand von . Der Abstand von  zu zu  ist nun größer als der Radius ist nun größer als der Radius 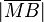 . .  liegt jedoch in liegt jedoch in 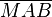 dem rechten Winkel gegenüber und muss demzufolge die längst der Seiten von dem rechten Winkel gegenüber und muss demzufolge die längst der Seiten von 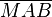 sein. sein.
Fall 2:
-
 liegt innerhalb von liegt innerhalb von  . .
Zurück zu: Serie 12 SoSe 2013
|  sei Tangente an den Kreis
sei Tangente an den Kreis  (Mittelpunkt
(Mittelpunkt  ) im Punkt
) im Punkt  . Beweisen Sie:
. Beweisen Sie: 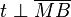 .
.
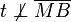 .
.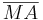 geben, die das Lot von
geben, die das Lot von  verschieden von
verschieden von 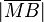 .
.  liegt jedoch in
liegt jedoch in 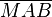 dem rechten Winkel gegenüber und muss demzufolge die längst der Seiten von
dem rechten Winkel gegenüber und muss demzufolge die längst der Seiten von 
